
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y=ax2+bx+c | … | t | m | ﹣2 | ﹣2 | n | … |
且当x=![]() 时,与其对应的函数值y>0,有下列结论:
时,与其对应的函数值y>0,有下列结论:
①abc<0;②m=n;③﹣2和3是关于x的方程ax2+bx+c=t的两个根;④![]() .
.
其中,正确结论的个数是( ).
A.1B.2C.3D.4
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
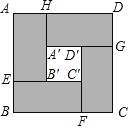
【题目】创客联盟的队员想用3D打印完成一幅边长为4米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形A′B′C′D′,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如下表
材料 | 甲 | 乙 |
价格(元/米2) | 60 | 30 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
(1)A′D′的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于3时,预备材料的购买资金700元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=8,P为线段AB上一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和PBFE,点P,C,E在一条直线上,∠DAP=60°,M,N分别是对角线AC,BE的中点,当点P在线段AB上移动时,点M,N之间的距离最短为( )
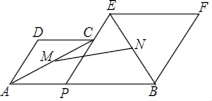
A. ![]() B.
B. ![]() C. 4D. 3
C. 4D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李驾驶小汽车匀速地从A地行驶到B地,行驶里程为360千米,设小汽车的行驶时间为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数表达式(不用写取值范围);
(2)小李上午8点驾驶小汽车从A地出发.
①小李需在当天12点至13点间到达B地,求小汽车行驶速度v的范围.
②小李能否在当天11点30分前到达B地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程mx2+(2m+1)x+m=0有两个实数根.
(1)求m的取值范围
(2)是否存在实数m,使方程的两实数根的倒数和为0?若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
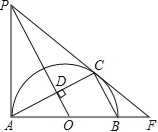
(1)求证:PC是半⊙O的切线;
(2)若∠CAB=30°,AB=10,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
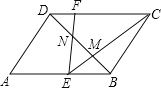
①E为AB的中点;
②FC=4DF;
③S△ECF=![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com