
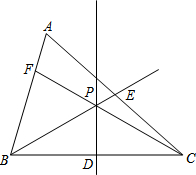
 如图所示,直线PD为△ABC一边BC的垂直平分线,点D为垂足,连接CP并延长CP交边AB于点F,射线BP交边AC于点E.
如图所示,直线PD为△ABC一边BC的垂直平分线,点D为垂足,连接CP并延长CP交边AB于点F,射线BP交边AC于点E.分析 (1)作BG⊥CF于点G,CH⊥BE于点H,然后根据全等三角形的判定方法,判断出△BGF≌△CHE,即可证明BF=CE.
(2)首先根据全等三角形的判定方法,判断出△BGP≌△BDP,所以PG=PD;然后根据全等三角形的判定方法,判断出△BGP≌△CHP,所以PG=PH;进而判断出PE+PF=2PD即可.
(3)首先根据∠PCD=30°,可得PC=2PD=2CD$÷\sqrt{3}$=BC$÷\sqrt{3}$=8$\sqrt{3}÷\sqrt{3}$=8,据此求出PE+PF=8;然后在△PEF中,利用余弦定理,求出PE、PF的关系,再根据PF>PE,求出PF的长是多少;在△PBF中,利用余弦定理,求出BF的长度是多少;最后在△AEF和△ABE中,利用余弦定理,求出AF的长是多少即可.
解答 (1)证明:如图,作BG⊥CF于点G,CH⊥BE于点H,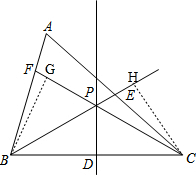 ,
,
∵∠A=∠BPF,
∴∠BFP=∠BEA=∠CEH,
∵直线PD为△ABC一边BC的垂直平分线,
∴PB=PC,∠BPF=∠CPE,
∴BG=CH,
∵$\left\{\begin{array}{l}{BG=CH}\\{∠BPG=∠CEH}\\{∠BGF=∠CHE}\end{array}\right.$,
∴△BGF≌△CHE,
∴BF=CE.
(2)解:∵∠A=60°,∠A=∠BPF,
∴∠BPF=60°,BP=CP,
∴∠PBD=∠PCD=30°,
∴∠GBP=∠PBD=30°,
∵$\left\{\begin{array}{l}{BP=CP}\\{∠BGP=90°}\\{∠BDP=90°}\end{array}\right.$,
∴△BGP≌△BDP,
∴PG=PD.
∵$\left\{\begin{array}{l}{BG=CH}\\{BP=CP}\\{∠BPG=∠CPH}\end{array}\right.$,
∴△BGP≌△CHP,
∴PG=PH,
∴PE+PF=PE+(PG+GF)=PG+(PE+GF)=PG+(PE+EH)=2PD,
即PE+PF=2PD;
(3)∵∠PCD=30°,
∴PC=2PD=2CD$÷\sqrt{3}$=BC$÷\sqrt{3}$=8$\sqrt{3}÷\sqrt{3}$=8,
∴PE+PF=8…①,
在△PEF中,
PE2+PF2-2PE•PF•cos120°
=PE2+PF2+PE•PF
=EF2
=72
=49…②
由①②,可得
PF=5或3,
∵PF>PE,
∴PF=5,
即PF的长为5.
在△PBF中,
PB2+PF2-2PB•PF•cos60°
=82+52-8×5
=49
∴BF=7;
设AF=x,AE=y,
则$\left\{\begin{array}{l}{{x}^{2}{+y}^{2}-2xy•cos60°{=7}^{2}}\\{{{(x+7)}^{2}{+y}^{2}-2(x+7)y•cos60°=(8+3)}^{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=5\frac{4}{7}}\\{y=7\frac{6}{7}}\end{array}\right.$,
∴AF=5$\frac{4}{7}$.
故答案为:PE+PF=2PD.
点评 (1)此题主要考查了全等三角形的判定和性质的应用,要熟练掌握全等三角形判定的方法.
(2)此题还考查了线段垂直平分线的性质,以及余弦定理的应用,要熟练掌握.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:解答题
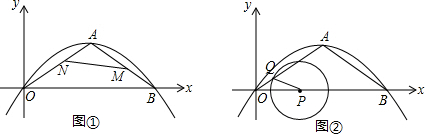
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
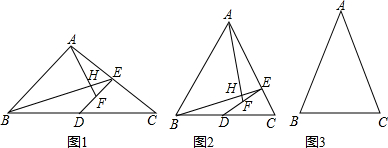
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com