
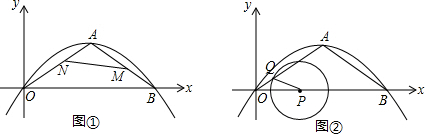
分析 (1)首先求出A、B两点的坐标,以及0A、0B、0C的长度,然后在△AOB中,利用余弦定理,求出cos∠AOB,进而求出∠AOB的度数是多少即可;
(2)根据题意,分两种情况讨论:①当动点M在BA上运动时,动点N在AO上运动;②当动点M在AO上运动时,动点N在OB上运动;然后根据三角形的面积的求法,求出△AMN的面积S与x之间的函数关系式即可;
(3)当⊙P与边AB只有1个公共点时,⊙P与边AB相切与点H,所以PH=PQ,然后分别用t表示出PH、PQ的值是多少,再解方程,求出t为何值时,⊙P与边AB只有1个公共点即可.
解答 解:(1)∵$y=\frac{1}{3}{x}^{2}+\frac{2\sqrt{3}}{3}x$
=$\frac{1}{3}$(${x}^{2}+2\sqrt{3}x+3$)-1
=${\frac{1}{3}(x+\sqrt{3})}^{2}$-1
∴A(-$\sqrt{3},1$);
令y=0,
则x=0或x=-2$\sqrt{3}$,
∴B(-2$\sqrt{3}$,0);
0A=$\sqrt{{(-\sqrt{3})}^{2}{+1}^{2}}$=2,OB=2$\sqrt{3}$,AB=$\sqrt{{(-\sqrt{3}-2\sqrt{3})}^{2}{+(1-0)}^{2}}$=2,
∵cos∠AOB=$\frac{{2}^{2}{+(2\sqrt{3})}^{2}{-2}^{2}}{2×2×2\sqrt{3}}$=$\frac{12}{8\sqrt{3}}=\frac{\sqrt{3}}{2}$,
∴∠AOB=30°.
(2)如图①,当动点M在BA上运动时,动点N在AO上运动,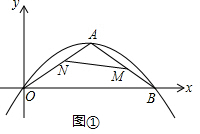 ,
,
动点M从点B点A的时间是:
2÷1=2(秒)
0<x≤2时,
∵0A=AB,
∴∠ABO=∠AOB=30°,
∴∠OAB=180°-30°-30°=120°;
∵AM=AB-MB=2-x,AN=x,
∴S=$\frac{1}{2}x(2-x)sin120°$=$\frac{\sqrt{3}}{4}x(2-x)$;
如图②,当动点M在AO上运动时,动点N在OB上运动,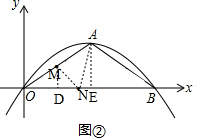 ,
,
动点M从点A点0的时间是:
2÷1=2(秒)
2<x≤4时,
∵$\frac{MD}{AE}=\frac{0M}{AO}=\frac{2-(t-2)}{2}=2-0.5t$,
∴MD=2-0.5t,
∵ON=t-2,
∴S=S△AON-S△MON
=$\frac{1}{2}(t-2)$$-\frac{1}{2}(t-2)(2-0.5t)$
=(0.5t-1)2
综上,可得S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{4}x(2-x),0<x≤2}\\{{(0.5t-1)}^{2},2<x≤4}\end{array}\right.$.
(3)如图③,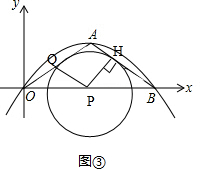 ,
,
当⊙P与边AB只有1个公共点时,⊙P与边AB相切与点H,
∴PH=PQ;
∵OQ=t,OP=$\sqrt{3}t$,∠A0B=30°,
∴${PQ}^{2}{=t}^{2}{+(\sqrt{3}t)}^{2}-2t•\sqrt{3}t•cos30°$
=t2,
∴PQ=t,
∵∠AB0=30°,
∴PH=$\frac{1}{2}$PB=$\frac{1}{2}(2\sqrt{3}-\sqrt{3}t)$,
∵PH=PQ,
∴$\frac{1}{2}(2\sqrt{3}-\sqrt{3}t)$=t,
解得t=4$\sqrt{3}$-6,
即t=4$\sqrt{3}$-6时,⊙P与边AB只有1个公共点.
点评 (1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力;
(2)此题还考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握.
(3)此题还考查了三角形的面积的求法,以及余弦定理的应用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
| x(公里) | 80 | 120 | 180 | 200 | … |
| y(元) | 200 | 300 | 450 | 500 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
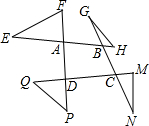 如图,以四边形ABCD各顶点及各边延长线上的点构成△AEF、△BGH、△CMN、△DPQ,求∠E+∠F+∠G+∠H+∠M+∠N+∠P+∠Q的度数.
如图,以四边形ABCD各顶点及各边延长线上的点构成△AEF、△BGH、△CMN、△DPQ,求∠E+∠F+∠G+∠H+∠M+∠N+∠P+∠Q的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
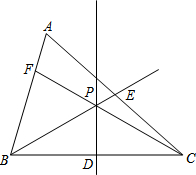 如图所示,直线PD为△ABC一边BC的垂直平分线,点D为垂足,连接CP并延长CP交边AB于点F,射线BP交边AC于点E.
如图所示,直线PD为△ABC一边BC的垂直平分线,点D为垂足,连接CP并延长CP交边AB于点F,射线BP交边AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
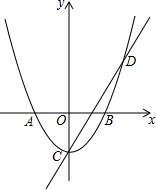 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com