
 (1)在直角坐标系中画出函数y=x2+x-6的图象;
(1)在直角坐标系中画出函数y=x2+x-6的图象;分析 (1)利用描点法画二次函数图象;
(2)结合图形即可得出答案;
(3)结合图形即可得出答案;
(4)根据二次函数y=x2+x-6的图象,则一元二次方程x2+x-6=-2的根为图象中y=-2时x的值.
解答 解:(1)由y=x2+x-6知,该抛物线的顶点坐标是(-$\frac{1}{2}$,-$\frac{25}{4}$),抛物线的开口方向向上.
由y=-x2+4x-2知抛物线与y轴的交点坐标是(0,-6).
当y=0时,x2+x-6=0,
解得x1=-3,x2=2.
则该抛物线与x轴的交点坐标是(-3,0),(2,0).
故该抛物线的图象如图所示: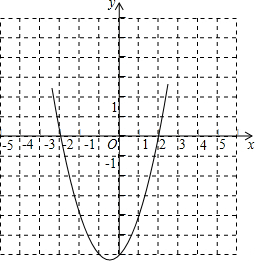
(2)根据图象可得:抛物线的对称轴是x=-$\frac{1}{2}$,开口向上,与x轴的交点坐标是(2,0)(-3,0),顶点坐标是(-$\frac{1}{2}$,-$\frac{25}{4}$),
则当x>-$\frac{1}{2}$时,y随x的增大而增大,
当x<-3或x>2时,y>0.
故答案为$>-\frac{1}{2}$,x<-3或x>2.
(3)当-1≤x≤2时,y的范围是-$\frac{25}{4}$≤y≤0.
故答案为:-$\frac{25}{4}$≤y≤0.
(4)作出二次函数y=x2-6x+4的图象如图,由图中可以看出,当y=-2时,对应的x的值,即方程的根.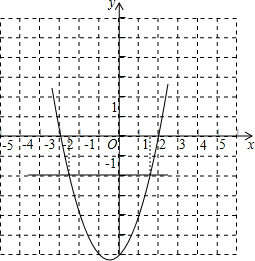
点评 此题考查了二次函数的图象,解题的关键是能综合利用二次函数的对称轴、开口方向、与x轴的交点坐标、顶点坐标等得出不等式的解集.也考查了二次函数图象与一元二次方程根的关系;关键是得到一元二次方程的图象;难点是判断出一元二次方程的根在图象中的位置.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
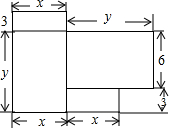 小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).
小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
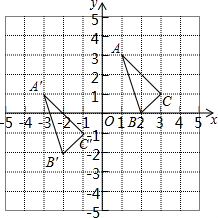 △ABC与△A′B′C′在平面直角坐标系中的位置如图.
△ABC与△A′B′C′在平面直角坐标系中的位置如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程x2+4x+5=0,则x1+x2=-4,x1x2=5 | |
| B. | 方程2x2-3x+m=0有实根,则m≤$\frac{9}{8}$ | |
| C. | 方程x2-8x+1=0可配方得(x-4)2=15 | |
| D. | 方程x2+x-1=0两根x1=$\frac{{-1+\sqrt{5}}}{2}$,x2=$\frac{{-1-\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
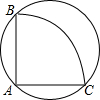 如图有一个直径为8的圆形铁皮,要从中剪出一个圆心角为90°的最大扇形ABC,用此剪下的扇形铁皮围成一个圆锥的侧面,则此圆锥的高为$\sqrt{30}$(结果保留根号).
如图有一个直径为8的圆形铁皮,要从中剪出一个圆心角为90°的最大扇形ABC,用此剪下的扇形铁皮围成一个圆锥的侧面,则此圆锥的高为$\sqrt{30}$(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
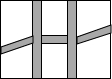 某单位院内有一块长30m,宽20m的矩形空地,准备将其建成一个矩形花坛,要求在花坛中修两条纵向平行和横向弯折的小道(如图),剩余的地方种植花草,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:左右小道进出口的宽度相等,且每段小道均为平行四边形)
某单位院内有一块长30m,宽20m的矩形空地,准备将其建成一个矩形花坛,要求在花坛中修两条纵向平行和横向弯折的小道(如图),剩余的地方种植花草,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:左右小道进出口的宽度相等,且每段小道均为平行四边形)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com