
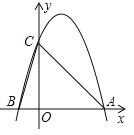
【题目】如图所示,二次函数![]() 的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中![]() ,
,![]() ),使
),使![]() ,求点D的坐标.
,求点D的坐标.
【答案】(1)3;(2)B(-1,0);(3)D(2,3).
【解析】
试题(1)由二次函数![]() 的图象与x轴的一个交点为A(3,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;
的图象与x轴的一个交点为A(3,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;
(2)根据(1)求得二次函数的解析式,然后将y=0代入函数解析式,即可求得点B的坐标;
(3)根据(2)中的函数解析式求得点C的坐标,由二次函数图象上有一点D(x,y)(其中x>0,y>0),可得点D在第一象限,又由![]() ,可知点D与点C的纵坐标相等,代入函数的解析式即可求得点D的坐标.
,可知点D与点C的纵坐标相等,代入函数的解析式即可求得点D的坐标.
试题解析:(1)∵二次函数![]() 的图象与x轴的一个交点为A(3,0),∴
的图象与x轴的一个交点为A(3,0),∴![]() ,解得:
,解得:![]() ;
;
(2)∵二次函数的解析式为:![]() ,∴当
,∴当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,![]() ,∴B(﹣1,0);
,∴B(﹣1,0);
(3)如图,连接BD、AD,过点D作DE⊥AB,∵当x=0时,y=3,∴C(0,3),若![]() ,∵D(x,y)(其中x>0,y>0),则可得OC=DE=3,∴当y=3时,
,∵D(x,y)(其中x>0,y>0),则可得OC=DE=3,∴当y=3时,![]() ,解得:x=0或x=2,∴点D的坐标为(2,3).
,解得:x=0或x=2,∴点D的坐标为(2,3).
另法:点D与点C关于x=1对称,故D(2,3).


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
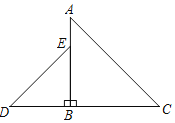
【题目】如图,△ABC、△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=![]() .将△BDE绕点B逆时针方向旋转后得△BD'E',当点E'恰好落在线段AD'上时,则CE'=_______.
.将△BDE绕点B逆时针方向旋转后得△BD'E',当点E'恰好落在线段AD'上时,则CE'=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销的太阳路灯,标价为4000元/个,促销活动期间,其优惠方法如下:
A.一次性购买数量不超过80个,按标价收费;
B.一次性购买数量超过80个,每多买一个,所购路灯每个可降价8元,但单价最低不能低于3200元/个.
(1)购买80个这样的路灯,应需付款_________________元.
(2)若一顾客一次性购买这样的路灯用去516000元,则该顾客实际购买了多少个这样的路灯.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON,点A在射线OM上.根据下列方法画图.
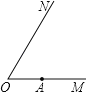
①以O为圆心,OA长为半径画圆,交ON于点B,交射线OM的反向延长线于点C,连接BC;
②以OA为边,在∠MON的内部,画∠AOP=∠OCB;
③连接AB,交OP于点E;
④过点A作⊙O的切线,交OP于点F.
(1)依题意补全图形;
(2)求证∠MOP=∠PON;
(3)若∠MON=60°,OF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
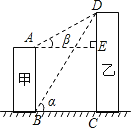
【题目】如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从B点测得D点的仰角α为60°从A点测得D点的仰角β为30°,已知甲建筑物高AB=36米.
(1)求乙建筑物的高DC;
(2)求甲、乙两建筑物之间的距离BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点BD是对角线,AG∥DB,交CB的延长线于G,连接GF,若AD⊥BD.下列结论:①DE∥BF;②四边形BEDF是菱形;③FG⊥AB;④S△BFG=![]() .其中正确的是( )
.其中正确的是( )

A. ①②③④ B. ①② C. ①③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE.
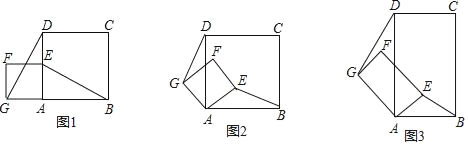
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ;②直线DG与直线BE之间的位置关系是 .
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快餐店共有10名员工,所有员工工资的情况如下表:
人员 | 店长 | 厨师甲 | 厨师乙 | 会计 | 服务员甲 | 服务员乙 | 勤杂工 |
人数 | 1 | 1 | 1 | 1 | 1 | 3 | 2 |
工资额 | 20000 | 7000 | 4000 | 2500 | 2200 | 1800 | 1200 |
请解答下列问题:
(1)餐厅所有员工的平均工资是 ;所有员工工资的中位数是 .
(2)用平均数还是用中位数描述该餐厅员工工资的一般水平比较恰当?
(3)去掉店长和厨师甲的工资后,其他员工的平均工资是多少?它是否也能反映该快餐店员工工资的一般水平?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com