
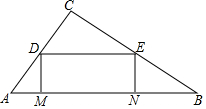
 如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N做AB的垂线,分别交两直角边于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外).
如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N做AB的垂线,分别交两直角边于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外).分析 (1)根据△ABC∽△ADM∽△DEC∽△EBN,可得共有6组不同的相似三角形;
(2)根据△ADM∽△ABC,AM=t,可得$\frac{AM}{AC}$=$\frac{MD}{BC}$,即$\frac{t}{3}$=$\frac{DM}{4}$,即可得出DM=$\frac{4}{3}$t,EN=DM=$\frac{4}{3}$t,再根据△BEN∽△BAC,得出$\frac{BN}{BC}$=$\frac{EN}{AC}$,即$\frac{BN}{4}$=$\frac{\frac{4}{3}t}{3}$,进而得到NB=$\frac{16}{9}$t,据此可得点N的运动速度:$\frac{16}{9}$t÷t=$\frac{16}{9}$;
(3)当点N、M相遇时,有$\frac{16}{9}$t+t=5,解得t=$\frac{9}{5}$;当点N、M相遇后继续运动,点N先到达A点,此时点M停止运动,则有$\frac{16}{9}$t=5,解得t=$\frac{45}{16}$,若矩形DENM为正方形,则DM=MN,分两种情况:①相遇前;②相遇后,分别根据DM=MN列出关于t的方程,求得t的值即可.
解答 解:(1)∵四边形DENM为矩形,
∴DE∥AB,∠AMD=∠ENB=90°,
∵∠C=90°,
∴∠AMD=∠ENB=∠C=90°,
∴△ABC∽△ADM∽△DEC∽△EBN,
∴共有6组不同的相似三角形,
故答案为:6;
(2)在△ABC中,∠C=90°,AC=3,BC=4,
∴AB=5,
∵在运动过程中四边形DENM总为矩形,
∴∠AMD=∠BNE=90°,
∴△ADM∽△ABC,
由题得:AM=t,
∴$\frac{AM}{AC}$=$\frac{MD}{BC}$,即$\frac{t}{3}$=$\frac{DM}{4}$,
∴DM=$\frac{4}{3}$t,
∴EN=DM=$\frac{4}{3}$t,
同理可得,△BEN∽△BAC,
∴$\frac{BN}{BC}$=$\frac{EN}{AC}$,即$\frac{BN}{4}$=$\frac{\frac{4}{3}t}{3}$,
∴NB=$\frac{16}{9}$t,
∴点N的运动速度:$\frac{16}{9}$t÷t=$\frac{16}{9}$,
∴点N的运动速度为每秒$\frac{16}{9}$个单位长度;
(3)当点N、M相遇时,有$\frac{16}{9}$t+t=5,
解得t=$\frac{9}{5}$,
当点N、M相遇后继续运动,点N先到达A点,此时点M停止运动,
则有$\frac{16}{9}$t=5,
解得t=$\frac{45}{16}$,
若矩形DENM为正方形,则DM=MN,分两种情况:
①相遇前:当0<t<$\frac{9}{5}$时,DM=$\frac{4}{3}$t,MN=5-t-$\frac{16}{9}$t=5-$\frac{25}{9}$t,
∴$\frac{4}{3}$t=5-$\frac{25}{9}$t,
解得t=$\frac{45}{37}$;
②相遇后:当$\frac{9}{5}$<t≤$\frac{45}{16}$时,DM=$\frac{3}{4}$(5-t),MN=t-$\frac{9}{16}$(5-t),
∴$\frac{3}{4}$(5-t)=t-$\frac{9}{16}$(5-t),
解得t=$\frac{105}{37}$>$\frac{45}{16}$(舍去),
综上所述,当t=$\frac{45}{37}$时,矩形DENM为正方形.
点评 本题属于三角形综合题,主要考查了相似三角形的判定与性质,矩形的性质以及正方形的性质的综合应用,解决问题的关键是根据相似三角形的对应边成比例列出比例式进行计算.解题时注意分类思想的运用.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
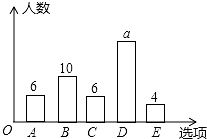 为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该图中a的值是( )
为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该图中a的值是( )| A. | 28 | B. | 26 | C. | 24 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
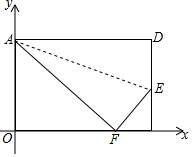 折叠矩形ABCD的一边AD,折痕为AE且使D落BC边上的点F处,已知AB=8cm,BC=10cm,则点F的坐标是(6,0),点E的坐标是(10,3).
折叠矩形ABCD的一边AD,折痕为AE且使D落BC边上的点F处,已知AB=8cm,BC=10cm,则点F的坐标是(6,0),点E的坐标是(10,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 北京 | 武汉 | 广州 | 哈尔滨 |
| 平均气温(单位℃) | -2.6 | 5.8 | 13.1 | -9.4 |
| A. | 北京 | B. | 武汉 | C. | 广州 | D. | 哈尔滨 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9x+25y}{25+y}$ | B. | $\frac{x+9}{2}$ | C. | $\frac{25x+9y}{25+y}$ | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com