
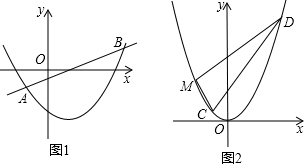
���� ��1�����������ߵĶ���ʽ����ֱ�ӵó������ߵĽ���ʽ��
��2��������ֱ�ߺ������߽���ʽ���������ɹ���x��һԪ���η��̣�����A��x1��y1����B��x2��y2�����ɸ���ϵ���Ĺ�ϵ�����x1+x2=4k+2��x1x2=9���ٸ��������ɵõ�����k�ķ��̣������k��ֵ����ͬ������k=1ʱ���ɵõ�����b�ķ��̣������b��ֵ��
��3����ƽ�ƿ����������C1�Ľ���ʽ��������M�����꣬��C��x1��y1����D��x2��y2��������M��l��y�ᣬ����C��CE��l��E������D��DF��l��F����֤��Rt��DFM��Rt��MEC�������������ε����ʣ������ɵ�4��x1+x2��-x1x2=32����ֱ��CD�Ľ���ʽΪy=kx+b������ֱ��CD��������C1�Ľ���ʽ���������ɹ���x��һԪ���η��̣����ɸ���ϵ���Ĺ�ϵ�ɵõ�b��k�Ĺ�ϵ�������ô𰸣�
��� �⣺��1����������C��y=$\frac{1}{4}$x2+bx+c�Ķ��㣨1��-2����
�������߽���ʽΪy=-$\frac{1}{4}$��x-1��2-2��
��2���ٵ�b=-4ʱ��ֱ��l����ʽΪy=kx-4��
����$\left\{\begin{array}{l}{y=\frac{1}{4}��x-1��^{2}-2}\\{y=kx-4}\end{array}\right.$��������x2-��4k+2��x+9=0��
��A��x1��y1����B��x2��y2����
��AB��x��ƽ�֣�
��y1+y2=0��
��x1+x2=4k+2��x1x2=9��
��y1+y2=k��x1+x2��-8=k��4k+2��-8=0�����k=$\frac{-1��\sqrt{33}}{4}$��
�ڵ�k=1ʱ��ֱ��l����ʽΪy=x+b��
����$\left\{\begin{array}{l}{y=\frac{1}{4}��x-1��^{2}-2}\\{y=x+b}\end{array}\right.$��������x2-6x-7-4b=0��
��x1+x2=6��x1x2=-7-4b��
��k=1ʱ��AB=$\sqrt{2}$��x2-x1��=$\sqrt{2}$$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$$\sqrt{64+16b}$��
��AB=4$\sqrt{10}$��
��$\sqrt{2}$$\sqrt{64+16b}$=4$\sqrt{10}$�����b=1��
��3���������֪������C1�Ľ���ʽΪy=$\frac{1}{4}$x2��
��M��-4��4����
��C��x1��y1����D��x2��y2����
����M��l��y�ᣬ����C��CE��l��E������D��DF��l��F����ͼ��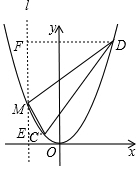
��MD��MC��
���MDC=90�㣬
���FDM+��DMF=��DMF+��CME��
���FDM=��CME���ҡ�DFM=��CEM=90�㣬
��Rt��DFM��Rt��MEC��
��$\frac{DF}{ME}$=$\frac{FM}{EC}$����$\frac{{x}_{2}+4}{4-{y}_{1}}$=$\frac{{y}_{2}-4}{{x}_{1}+4}$��
�ߵ�C��D��������C1�ϣ�
��$\frac{{x}_{2}+4}{4-\frac{1}{4}{{x}_{1}}^{2}}$=$\frac{\frac{1}{4}{{x}_{2}}^{2}-4}{{x}_{1}+4}$��������4��x1+x2��-x1x2=32��
��ֱ��CD�Ľ���ʽΪy=kx+b��
����$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y=kx+b}\end{array}\right.$��������x2-4kx-4b=0��
��x1+x2=4k��x1x2=-4b��
��4��4k-��-4b��=32�������ɵ�b=8-4k
��ֱ��CD����ʽΪy=kx+b=kx-4k+8=k��x-4��+8��
��ֱ��CD�����㣨4��8����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ����������ͼ��Ľ��㡢����ϵ���Ĺ�ϵ�����������ε��ж������ʼ�����˼���֪ʶ���ڣ�1����ע�������߶���ʽ��Ӧ�ã��ڣ�2������ƽ�ֻ��߶εij��ȵõ�����k��b�ķ����ǽ���Ĺؼ���ע�����ϵ����ϵ��Ӧ�ã��ڣ�3���й������������ƣ������������ε����ʽ�ϸ���ϵ���Ĺ�ϵ�õ�b��k�Ĺ�ϵ�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�


 �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x}{2}$��$\frac{1}{x}$ | B�� | -m3��n3 | C�� | $\frac{2}{3}$a2b��2ab2 | D�� | 22��32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
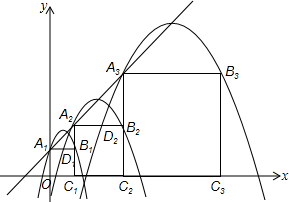 ��ƽ��ֱ������ϵxOy�У�������A1B1C1O��A2B2C2C1��A3B3C3C2����������ͼ�ķ�ʽ���ã���A1��A2��A3������An�͵�C1��C2��C3������Cn�ֱ�����ֱ��y=x+1��x���ϣ�������L1����A1��B1���Ҷ�����ֱ��y=x+1�ϣ�������L2����A2��B2���Ҷ�����ֱ��y=x+1�ϣ��������˹��ɣ�������Ln����An��Bn���Ҷ���Ҳ��ֱ��y=x+1�ϣ�����������L2��������A1B1C1O�ı�A1B1�ڵ�D1��������L3��������A2B2C2C1�ı�A2B2�ڵ�D2������������Ln+1��������AnBnCnCn-1�ı�AnBn�ڵ�Dn������n��2��nΪ����������
��ƽ��ֱ������ϵxOy�У�������A1B1C1O��A2B2C2C1��A3B3C3C2����������ͼ�ķ�ʽ���ã���A1��A2��A3������An�͵�C1��C2��C3������Cn�ֱ�����ֱ��y=x+1��x���ϣ�������L1����A1��B1���Ҷ�����ֱ��y=x+1�ϣ�������L2����A2��B2���Ҷ�����ֱ��y=x+1�ϣ��������˹��ɣ�������Ln����An��Bn���Ҷ���Ҳ��ֱ��y=x+1�ϣ�����������L2��������A1B1C1O�ı�A1B1�ڵ�D1��������L3��������A2B2C2C1�ı�A2B2�ڵ�D2������������Ln+1��������AnBnCnCn-1�ı�AnBn�ڵ�Dn������n��2��nΪ�����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a6��a2=a3 | B�� | a5-a2=a3 | ||
| C�� | ��3a3��2=6a9 | D�� | 2��a3b��2-3��a3b��2=-a6b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
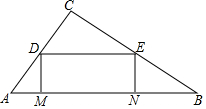 ��ͼ����ABC�У���C=90�㣬AC=3��BC=4�����߶�AB�ϣ�����M�ӵ�A�������B�������˶���ͬʱ����N��B�������A�������˶�������M��N����һ��ֹͣ�˶�ʱ����һ��Ҳֹͣ�˶����ֱ����M��N��AB�Ĵ��ߣ��ֱ���ֱ�DZ��ڵ�D��E������DE�����˶�ʱ��Ϊt�룬���˶��������ı���DENM��Ϊ���Σ���M��N�غϳ��⣩��
��ͼ����ABC�У���C=90�㣬AC=3��BC=4�����߶�AB�ϣ�����M�ӵ�A�������B�������˶���ͬʱ����N��B�������A�������˶�������M��N����һ��ֹͣ�˶�ʱ����һ��Ҳֹͣ�˶����ֱ����M��N��AB�Ĵ��ߣ��ֱ���ֱ�DZ��ڵ�D��E������DE�����˶�ʱ��Ϊt�룬���˶��������ı���DENM��Ϊ���Σ���M��N�غϳ��⣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| a/m | �� | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | �� |
| cm 2 | �� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�BD=CD��BE��AD��F��AE=EF����BE=7CE��AE=$\frac{5}{2}$����BF=$\frac{10}{3}$��
��ͼ���ڡ�ABC�У�BD=CD��BE��AD��F��AE=EF����BE=7CE��AE=$\frac{5}{2}$����BF=$\frac{10}{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com