
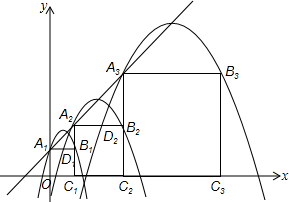
 ��ƽ��ֱ������ϵxOy�У�������A1B1C1O��A2B2C2C1��A3B3C3C2����������ͼ�ķ�ʽ���ã���A1��A2��A3������An�͵�C1��C2��C3������Cn�ֱ�����ֱ��y=x+1��x���ϣ�������L1����A1��B1���Ҷ�����ֱ��y=x+1�ϣ�������L2����A2��B2���Ҷ�����ֱ��y=x+1�ϣ��������˹��ɣ�������Ln����An��Bn���Ҷ���Ҳ��ֱ��y=x+1�ϣ�����������L2��������A1B1C1O�ı�A1B1�ڵ�D1��������L3��������A2B2C2C1�ı�A2B2�ڵ�D2������������Ln+1��������AnBnCnCn-1�ı�AnBn�ڵ�Dn������n��2��nΪ����������
��ƽ��ֱ������ϵxOy�У�������A1B1C1O��A2B2C2C1��A3B3C3C2����������ͼ�ķ�ʽ���ã���A1��A2��A3������An�͵�C1��C2��C3������Cn�ֱ�����ֱ��y=x+1��x���ϣ�������L1����A1��B1���Ҷ�����ֱ��y=x+1�ϣ�������L2����A2��B2���Ҷ�����ֱ��y=x+1�ϣ��������˹��ɣ�������Ln����An��Bn���Ҷ���Ҳ��ֱ��y=x+1�ϣ�����������L2��������A1B1C1O�ı�A1B1�ڵ�D1��������L3��������A2B2C2C1�ı�A2B2�ڵ�D2������������Ln+1��������AnBnCnCn-1�ı�AnBn�ڵ�Dn������n��2��nΪ�������������� ��1����ֱ�߽���ʽ�����A1�����꣬�������ε�����������B1���꣬����������A2�ĺ����꣬�������������꣬�����������ε����ʿ����B2�����꣬ͬ�������B3�����ꣻ
��2���ɶԳ��Կ���������ߵĶԳ��ᣬ�������䶥�����꣬�ٽ����֪����������������߽���ʽ����д��L2��L3�Ľ���ʽ������An��Bn�ı仯���ɣ������������Ln�Ķ������ꣻ
��3����������L2�Ľ���ʽ�����A1D1�ij���������k1��ͬ�������k2���Ӷ����������֮���������ϵ��
��� �⣺
��1����A1��ֱ��y=x+1�ϣ�
��A1��������0��1����
��A1B1=OA1=1��
��B1��1��1����
��A2������Ϊ1������ֱ��y=x+1�ϣ�
��A2��1��2����
��A2B2=A2C1=2��
��B2��3��2����ͬ��B3��7��4����
�ʴ�Ϊ����1��1������3��2������7��4����
��2��������L2��L3�Ľ���ʽ�ֱ�Ϊy=-��x-2��2+3��y=-$\frac{1}{2}$��x-5��2+6��
������L2�Ľ���ʽ�����������£�
����ֱ��y=x+1����x=0���ɵ�y=1��
��A1��0��1����
���ı���A1B1C1O�������Σ�
��C1��1��0�����ֵ�A2��ֱ��y=x+1�ϣ�
��ɵõ�A2��1��2����
�֡�B2������Ϊ��3��2����
��������L2�ĶԳ���Ϊֱ��x=2��
��������L2�Ķ���Ϊ��2��3����
��������L2�Ľ���ʽΪ��y=a��x-2��2+3��
��L2����B2��3��2����
��2=a����3-2��2+3�����a=-1��
��������L2�Ľ���ʽΪy=-��x-2��2+3��
����������Ln�Ķ�������Ϊ��3��2n-2-1��3��2n-2����
֤�����£�
��������AnBnCnCn-1����An��Bn���������ΪAn��2n-1-1��2n-1����Bn��2n-1��2n-1����
��������Ln�ĶԳ���Ϊֱ��x=$\frac{{2}^{n-1}-1+{2}^{n}-1}{2}$=3��2n-2-1���ֶ�����ֱ��y=x+1�ϣ�
��y=3��2n-2��
��������Ln�Ķ�������Ϊ��3��2n-2-1��3��2n-2����
��3��k1��k2��������ϵΪk1=k2��
�������£�
�ɣ�2����L2�Ľ���ʽΪy=-��x-2��2+3��
��y=1ʱ��1=-��x-2��2+3�����x1=2-$\sqrt{2}$��x2=2+$\sqrt{2}$��
��0��A1D1��1��
��x=2-$\sqrt{2}$��
��A1D1=2-$\sqrt{2}$=$\sqrt{2}$��$\sqrt{2}$-1����
��D1B1=1-��2-$\sqrt{2}$��=$\sqrt{2}$-1��
��A1D1=$\sqrt{2}$•D1B1����k1=$\sqrt{2}$��
ͬ�������A2D2=4-2 $\sqrt{2}$=2 $\sqrt{2}$��$\sqrt{2}$-1����
D2B2=2-��4-2 $\sqrt{2}$��=2 $\sqrt{2}$-2=2��$\sqrt{2}$-1����
��A2D2=$\sqrt{2}$•D2B2����k2=$\sqrt{2}$��
��k1=k2��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰�����ε����ʡ�����ͼ���ϵ����������������ϵ����������ͼ��Ľ����֪ʶ���ڣ�1�������An�ĺ������ǽ���Ĺؼ���ע�����������ʵ�Ӧ�ã��ڣ�2�������ô���ϵ��������������߽���ʽ���������߶�������ʱע����仯���ɣ��ڣ�3�������ú���ͼ��Ľ��������Ӧ�߶εij��ֱ����k1��k2��ֵ�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{x-1}$ | B�� | $\frac{1}{1-x}$ | C�� | $\frac{1-2x}{x-1}$ | D�� | $\frac{2x-1}{x-1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
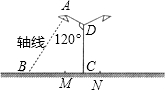 Ҫ�ڿ�Ϊ36m�Ĺ�·���̻���MN����Ϊ4m�������밲װ·�ƣ�·�ƵĵƱ�AD�ij�Ϊ3m���������CD��120�㣨��ͼ��ʾ����·�Ʋ���Բ�ε��֣����ֵ�����AB��Ʊ۴�ֱ�������ֵ�����ͨ����··��һ����м�ʱ����ȥ�̻�����·�沿�֣�������Ч�������룬�ʣ�Ӧ��ƶ�ߵĵ���������ȡ�������������Ч��������ȷ��0.01m���ο�����$\sqrt{3}$��1.732��
Ҫ�ڿ�Ϊ36m�Ĺ�·���̻���MN����Ϊ4m�������밲װ·�ƣ�·�ƵĵƱ�AD�ij�Ϊ3m���������CD��120�㣨��ͼ��ʾ����·�Ʋ���Բ�ε��֣����ֵ�����AB��Ʊ۴�ֱ�������ֵ�����ͨ����··��һ����м�ʱ����ȥ�̻�����·�沿�֣�������Ч�������룬�ʣ�Ӧ��ƶ�ߵĵ���������ȡ�������������Ч��������ȷ��0.01m���ο�����$\sqrt{3}$��1.732���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
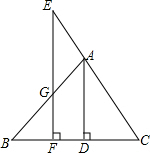 ��ͼ����֪AD��BC�ڵ�D��EF��BC�ڵ�F����AB�ڵ�G����CA���ӳ����ڵ�E����E=��AGE����֤����BAD=��CAD��
��ͼ����֪AD��BC�ڵ�D��EF��BC�ڵ�F����AB�ڵ�G����CA���ӳ����ڵ�E����E=��AGE����֤����BAD=��CAD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3+a3=a6 | B�� | 5a5-a5=4a5 | C�� | ��2a��3=6a3 | D�� | a8��a2=a4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
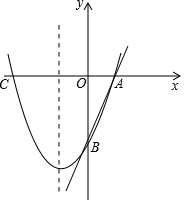 ��ͼ����ֱ֪��y=3x-3�ֱ�x�ᡢy����A��B���㣬������y=x2+bx+c����
��ͼ����ֱ֪��y=3x-3�ֱ�x�ᡢy����A��B���㣬������y=x2+bx+c�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{4}{25}}=��\frac{2}{5}$ | B�� | $\sqrt{{{��{-3}��}^2}}=-3$ | C�� | -a2û��ƽ���� | D�� | $-\sqrt{{{��{-4}��}^2}}=-4$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com