
| A. | $\sqrt{\frac{4}{25}}=±\frac{2}{5}$ | B. | $\sqrt{{{({-3})}^2}}=-3$ | C. | -a2没有平方根 | D. | $-\sqrt{{{({-4})}^2}}=-4$ |
分析 根据算术平方根和平方根的性质求解即可.
解答 解:A、$\sqrt{\frac{4}{25}}$=$\frac{2}{5}$,故选项错误;
B、$\sqrt{(-3)^{2}}$=3,故选项错误;
C、a=0时,-a2的平方根是0,故选项错误;
D、-$\sqrt{(-4)^{2}}$=-4,故选项正确.
故选:D.
点评 此题主要考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:①被开方数a是非负数;②算术平方根a本身是非负数.求一个非负数的算术平方根与求一个数的平方互为逆运算,在求一个非负数的算术平方根时,可以借助乘方运算来寻找.还考查了平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.


科目:初中数学 来源: 题型:解答题
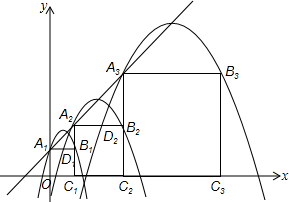 在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a/m | … | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| cm 2 | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,AE=$\frac{5}{2}$,则BF=$\frac{10}{3}$.
如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,AE=$\frac{5}{2}$,则BF=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 6 | C. | -10 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是二次函数y=ax2+bx+c的图象,则下列判断正确的有( )
如图,是二次函数y=ax2+bx+c的图象,则下列判断正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com