
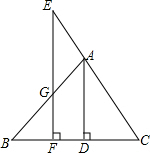
 如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠E=∠AGE,求证:∠BAD=∠CAD.
如图,已知AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠E=∠AGE,求证:∠BAD=∠CAD. 科目:初中数学 来源: 题型:解答题
| 每月每户用水量 | 每吨价(元) |
| 不超过10吨部分 | 0.50 |
| 超过10吨而不超过20吨部分 | 0.75 |
| 超过20吨部分 | 1.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
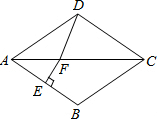 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 80° | B. | 70° | C. | 65° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
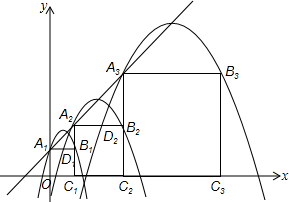 在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 6 | C. | -10 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com