
分析 (1)先根据题意画出树状图,再得出不同的选择方案;
(2)根据在第二组四个项目中各任意选取另外一个画树状图,即可得出共有16种不同情况,其中必胜和必成选择同种方案有4种,据此可得必胜和必成选择同种方案的概率.
解答 解:(1)由题可得树状图:
∴每位男考生一共有8种不同的选择方案,
故答案为:8;
(2)在第二组四个项目中各任意选取另外一个,画树状图如下: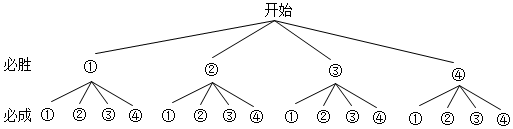
共有16种不同情况,其中必胜和必成选择同种方案有4种,
∴必胜和必成选择同种方案的概率=$\frac{4}{16}$=$\frac{1}{4}$.
点评 本题主要考查了列表法与画树状图法,解题时注意:求概率的关键在于列举出所有可能的结果,列表法是一种,但当一个事件涉及三个或更多元素时,为不重不漏地列出所有可能的结果,通常采用树形图.


科目:初中数学 来源: 题型:解答题
| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 年销售量y(万件) | 5.5 | 5 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
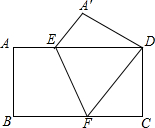 如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.
如图:把一个矩形如图折叠,使顶点B和D重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
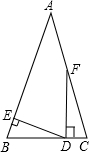 如图,已知△ABC中,∠B=∠C,D是边BC上一点,DE⊥AB,垂足为点E,DF⊥BC,DF交边AC于点F,∠AFD=155°,则∠EDF=65°.
如图,已知△ABC中,∠B=∠C,D是边BC上一点,DE⊥AB,垂足为点E,DF⊥BC,DF交边AC于点F,∠AFD=155°,则∠EDF=65°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com