
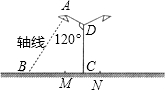
 要在宽为36m的公路的绿化带MN(宽为4m)的中央安装路灯,路灯的灯臂AD的长为3m,且与灯柱CD成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线AB与灯臂垂直.当灯罩的轴线通过公路路面一侧的中间时(除去绿化带的路面部分),照明效果最理想,问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m,参考数据$\sqrt{3}$≈1.732)
要在宽为36m的公路的绿化带MN(宽为4m)的中央安装路灯,路灯的灯臂AD的长为3m,且与灯柱CD成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线AB与灯臂垂直.当灯罩的轴线通过公路路面一侧的中间时(除去绿化带的路面部分),照明效果最理想,问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m,参考数据$\sqrt{3}$≈1.732) 分析 延长BA,CD交于点P,解直角三角形得到AP=PD•cos30°和BC的长,通过△PAD∽△PCB,得出$\frac{AP}{PC}$=$\frac{AD}{BC}$,代入数据即可得到结论.
解答 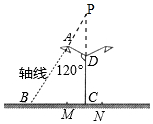 解:如图,延长BA,CD交于点P,
解:如图,延长BA,CD交于点P,
∵∠PAD=∠PCB=90°,∠ADC=120°,
∴∠P=30°,
∵AD=3,
∴PD=6,AP=PD•cos30°=3$\sqrt{3}$,
BC=(18-2)÷2+2=10.
∵∠P=∠P,∠PAD=∠PCB=90°,
∴△PAD∽△PCB,
∴$\frac{AP}{PC}$=$\frac{AD}{BC}$,
∴PC=$\frac{AP•BC}{AD}$=10$\sqrt{3}$m,
∴CD=PC-PD=10$\sqrt{3}$-6≈11.32m.
则应设计11.32m高的灯柱,才能取得最理想的照明效果.
点评 本题考查了相似三角形的性质,直角三角形的性质,锐角三角函数的概念,正确的作出辅助线构造相似三角形是解题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{2}$与$\frac{1}{x}$ | B. | -m3与n3 | C. | $\frac{2}{3}$a2b与2ab2 | D. | 22与32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
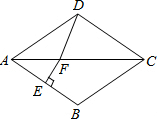 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 80° | B. | 70° | C. | 65° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
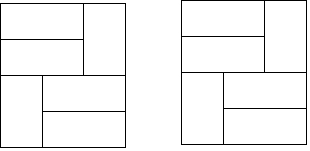
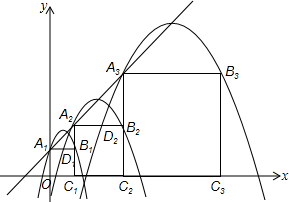 在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).
在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,…,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…,抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥2且n为正整数).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,AE=$\frac{5}{2}$,则BF=$\frac{10}{3}$.
如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,AE=$\frac{5}{2}$,则BF=$\frac{10}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com