
分析 由$\frac{1}{m}$-$\frac{1}{n}$=3两边都乘以mn得n-m=3mn,先计算括号内异分母分式的加法、同时将分子、分母因式分解,再计算括号内分式的乘法、加法,最后约分即可化简原式,将n-m=3mn代入可得答案.
解答 解:将$\frac{1}{m}$-$\frac{1}{n}$=3两边都乘以mn,得:n-m=3mn,
原式=[$\frac{2}{(m+n)^{3}}$•$\frac{m+n}{mn}$+$\frac{1}{(m+n)^{2}}$•$\frac{{m}^{2}+{n}^{2}}{{m}^{2}{n}^{2}}$]•$\frac{{m}^{3}{n}^{3}}{m-n}$
=[$\frac{2mn}{{m}^{2}{n}^{2}(m+n)^{2}}$+$\frac{{m}^{2}+{n}^{2}}{{m}^{2}{n}^{2}(m+n)^{2}}$]•$\frac{{m}^{3}{n}^{3}}{m-n}$
=$\frac{(m+n)^{2}}{{m}^{2}{n}^{2}(m+n)^{2}}$•$\frac{{m}^{3}{n}^{3}}{m-n}$
=$\frac{mn}{m-n}$,
将n-m=3mn代入上式,得:原式=$\frac{mn}{-3mn}$=-$\frac{1}{3}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算顺序和运算法则是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
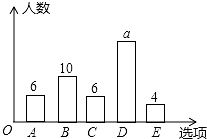 为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该图中a的值是( )
为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该图中a的值是( )| A. | 28 | B. | 26 | C. | 24 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{1-x}$ | C. | $\frac{1-2x}{x-1}$ | D. | $\frac{2x-1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
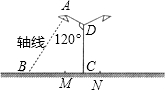 要在宽为36m的公路的绿化带MN(宽为4m)的中央安装路灯,路灯的灯臂AD的长为3m,且与灯柱CD成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线AB与灯臂垂直.当灯罩的轴线通过公路路面一侧的中间时(除去绿化带的路面部分),照明效果最理想,问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m,参考数据$\sqrt{3}$≈1.732)
要在宽为36m的公路的绿化带MN(宽为4m)的中央安装路灯,路灯的灯臂AD的长为3m,且与灯柱CD成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线AB与灯臂垂直.当灯罩的轴线通过公路路面一侧的中间时(除去绿化带的路面部分),照明效果最理想,问:应设计多高的灯柱,才能取得最理想的照明效果?(精确到0.01m,参考数据$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com