练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．化简$\frac{{x}^{2}}{x-1}$-x+1的结果是（　　）
    A．$\frac{1}{x-1}$B．$\frac{1}{1-x}$C．$\frac{1-2x}{x-1}$D．$\frac{2x-1}{x-1}$

    分析 根据分式加减运算的法则计算即可．

    解答 解：原式=$\frac{{x}^{2}}{x-1}$-$\frac{（x-1）^{2}}{x-1}$=$\frac{{x}^{2}-{x}^{2}+2x-1}{x-1}$=$\frac{2x-1}{x-1}$，
    故选D．

    点评 本题考查了分式的加减法，熟练掌握分式加减法的法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

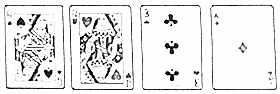    3．从一幅扑克牌（去掉大、小王）中任意抽取4张，根据牌面上的数字进行混合运算（每张牌只能用一次），使得运算结果为24或-24，其中红色扑克代表负数，黑色扑克代表正数，J、Q、K分别代表11，12，13．如果抽到的是下列四张扑克（一张黑Q，一张红Q，一张黑3，一张红A）凑成24所列的算式是12×3-（-12）×（-1）
    提示：【可运用加、减、乘、除、乘方（例如数2，6，可列62=36或26=64）运算，可用括号：注意：例如4×（1+2+3）=24与（2+1+3）×4=24只是顺序不同，属同一个算式】

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．阅读材料：黑白双雄，纵横江湖，双剑合璧，天下无敌，这是武侠小说中的常见描述，其意指两个人合在一起，取长补短，威力无比．在二次根式中也有这样相辅相成的例子．
    如（2+$\sqrt{3}$）（2-$\sqrt{3}$）=22-（-$\sqrt{3}$）2=1，（$\sqrt{5}$+$\sqrt{2}$）（$\sqrt{5}$-$\sqrt{2}$）=（$\sqrt{5}$）2-（$\sqrt{2}$）2=3，它们的积是有理数，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理数因素．于是，我们可以将下面的式子化简：
    $\frac{1}{2-\sqrt{3}}$=$\frac{2+\sqrt{3}}{（2-\sqrt{3}）（2+\sqrt{3}）}$=2+$\sqrt{3}$
    解决问题：
    （1）4+$\sqrt{7}$的一个有理化因式是4-$\sqrt{7}$．
    （2）计算：$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2015}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列属于同类项的是（　　）
    A．$\frac{x}{2}$与$\frac{1}{x}$B．-m3与n3C．$\frac{2}{3}$a2b与2ab2D．22与32

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．某市为了鼓励市民节约用水，规定自来水的收费标准如下表：
    每月每户用水量每吨价（元）
    不超过10吨部分0.50
    超过10吨而不超过20吨部分0.75
    超过20吨部分1.50
    （1）现已知小明家四月份用水22吨，应缴水费15.5元；
    （2）写出每月每户的水费y（元）与用水量x（吨）之间的关系式；
    （3）若小明家每月缴水费17元，问：他家该月用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．化简求值：[$\frac{2}{（m+n）^{3}}$•（$\frac{1}{m}$+$\frac{1}{n}$）+$\frac{1}{{m}^{2}+2mn+{n}^{2}}$•（$\frac{1}{{m}^{2}}$+$\frac{1}{{n}^{2}}$）]÷$\frac{m-n}{{m}^{3}{n}^{3}}$，其中，$\frac{1}{m}$-$\frac{1}{n}$=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

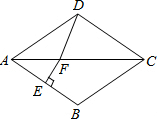    5．如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足，连结DF，则∠CDF等于（　　）
    A．80°B．70°C．65°D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

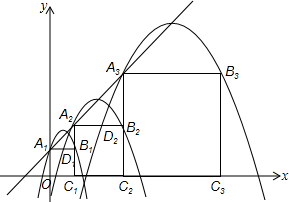    2．在平面直角坐标系xOy中，正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…，按如图的方式放置．点A1，A2，A3，…，An和点C1，C2，C3，…，Cn分别落在直线y=x+1和x轴上．抛物线L1过点A1，B1，且顶点在直线y=x+1上，抛物线L2过点A2，B2，且顶点在直线y=x+1上，…，按此规律，抛物线Ln过点An，Bn，且顶点也在直线y=x+1上，其中抛物线L2交正方形A1B1C1O的边A1B1于点D1，抛物线L3交正方形A2B2C2C1的边A2B2于点D2，…，抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn（其中n≥2且n为正整数）．
    （1）直接写出下列点的坐标：B1（1，1），B2（3，2），B3（7，4）；
    （2）写出抛物线L2、L3的解析式，并写出其中一个解析式求解过程，再猜想抛物线Ln的顶点坐标
    （3）设A1D1=k1•D1B1，A2D2=k2•D2B2，试判断k1与k2的数量关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知正方形的边长a（cm）    
    （1）正方形的面积S（cm2）与边长a（cm）的函数关系式为a2
    （2）用表格表示：
    a/m… $\frac{1}{2}$1$\frac{3}{2}$2$\frac{5}{2}$3…
    cm 2…      …
    （3）用图象表示：
    （4）根据以上三种表示方法回答问题；
    ①自变量的取值范围是什么？
     ②如何描述S随a的变化而变化的惰况？

    查看答案和解析>>

    同步练习册答案