练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

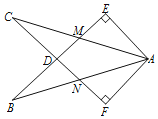
    【题目】如图，在Rt△AEB和Rt△AFC中，∠E=∠F=90°，BE=CF．BE与AC相交于点M，与CF相交于点D，AB与CF相交于点N，∠EAC=∠FAB．有下列结论：①∠B=∠C；②CD=DN；③CM=BN；④△ACN≌△ABM．其中正确结论的序号是________．

    【答案】①③④

    【解析】

    只要证明△ABE≌△ACF，△ACN≌△ABM即可判断．

    解：∵∠EAC＝∠FAB，

    ∴∠EAB＝∠CAF，

    在△ABE和△ACF，

    ，

    ∴△ABE≌△ACF（ASA），

    ∴∠B＝∠C．

    由△AEB≌△AFC知：∠B＝∠C，AC＝AB；

    在△ACN和△ABM，

    ，

    ∴△ACN≌△ABM（ASA）；（故④正确）

    ∴CM＝BN，

    由于条件不足，无法证得②CD＝DN；

    故答案为：①③④

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，一个正方体纸盒的棱长为6厘米，则它的表面积为　 　平方厘米．

    （2）将该正方体的一些棱剪开展成一个平面图形，则需要剪卉　 　条棱，并求这个平面图形的周长．

    （3）如图2，一个长方体纸盒的长、宽、高分别是a厘米、b厘米、c厘米（a＞b＞c）将它的一些棱剪开展成一个平面图形，求这个平面图形的最大周长，画出周长最大的平面图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=kx+b分别交x轴、y轴于A（1，0）、B（0，﹣1），交双曲线y=于点C、D．

    （1）求k、b的值；

    （2）写出不等式kx+b＞的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面内有任意一点和，按要求解答下列问题：

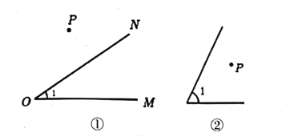
    （1）当点和外部时，如图①，过点作，，垂足分别为、，量一量和的度数，用数学式子表达它们之间的数量关系 ；

    （2）当点在内部时，如图②，以点为顶点作，使的两边分别和的两边垂直，垂足分别为、，用数学式子写出和的数量关系；

    （3）由上述情形，用文字语言叙述结论：如果一个角的两边分别和另一个角的两边垂直，那么这两个角 .

    （4）在图②中，若，求的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

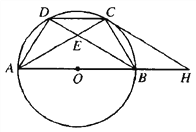
    【题目】如图，点A、B、C、D是直径为AB的⊙O上的四个点，CD＝BC，AC与BD交于点E。

    （1）求证：DC2＝CE·AC；

    （2）若AE＝2EC，求之值；

    （3）在（2）的条件下，过点C作⊙O的切线，交AB的延长线于点H，若S△ACH＝，求EC之长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

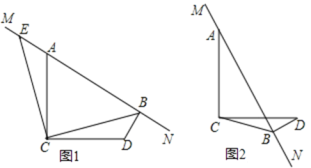
    【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC．

    (1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA．

    ①求证：点E在直线MN上；

    ②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想．

    (2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A，B两地相距450千米，两地之间有一个加油站O，且AO＝270千米，一辆轿车从A地出发，以每小时90千米的速度开往B地，一辆客车从B地出发，以每小时60千米的速度开往A地，两车同时出发，设出发时间为t小时．

    （1）经过几小时两车相遇？

    （2）当出发2小时时，轿车和客车分别距离加油站O多远？

    （3）经过几小时，两车相距50千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如：2÷2÷2，(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方，我们把 2÷2÷2 记作 2③，读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④，读作“-3 的圈 4 次方”.

    一般地，把（a≠0）记作a，记作“a 的圈c次方”.

    (1)直接写出计算结果：2③= ，(-3)④ = ，⑤= .

    (2)计算 24÷23 + (-8)×2③.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．诗中后两句的意思是：如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间房．

    （1）求该店有客房多少间？房客多少人？

    （2）假设店主李三公将客房进行改造后，房间数大大增加．每间客房收费20钱，且每间客房最多入住4人，一次性定客房18间以上（含18间），房费按8折优惠．若诗中“众客”再次一起入住，他们如何订房更合算？

    查看答案和解析>>

    同步练习册答案