
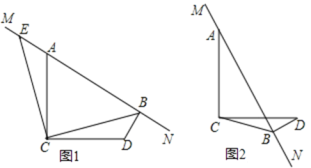
【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC.
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA.
①求证:点E在直线MN上;
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想.
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想.
【答案】(1)①见解析;②AB+BD=![]() BC,理由见解析;(2)ABBD=
BC,理由见解析;(2)ABBD=![]() BC,理由见解析;
BC,理由见解析;
【解析】
(1)①由四边形内角和定理得出∠CAB+∠CDB=180°,由旋转的性质得出△ECA≌△BCD,得出∠EAC=∠BDC,因此∠CAB+∠EAC=180°,即可得出结论;
②证出△ECB为等腰直角三角形,由勾股定理得出BE=![]() BC,再由BE=AE+AB,AE=BD,即可得出结论;
BC,再由BE=AE+AB,AE=BD,即可得出结论;
(2)过点C作CE⊥CB与MN交于点E,则∠ECB=90°,∠ACE=∠DCB,证出∠CAE=∠CDB,由ASA证明△ACE≌△DCB,得出AE=DB,EC=BC,证出△ECB为等腰直角三角形,由勾股定理得出EB=![]() BC,即可得出结论.
BC,即可得出结论.
(1)①证明:∵DB⊥MN,
∴∠ABD=90,在四边形ACDB中,
∵∠ACD=90
∴∠ACD+∠ABD=180
∴∠CAB+∠CDB=180
由旋转的性质得:△ECA≌△BCD
∴∠EAC=∠BDC,
∴∠CAB+∠EAC=180
∴点E在直线MN上
②解:AB+BD=![]() BC,理由如下:
BC,理由如下:
∵∠ACD=90
∴∠ACB+∠BCD=90
由①知∠ECA=∠BCD,EC=BC
∴∠ECB=∠ECA+∠ACB=90
∴△ECB为等腰直角三角形
∴BE=![]() BC
BC
∵BE=AE+AB
由①知AE=BD
∴AB+BD=![]() BC.
BC.
(2)解:ABBD=![]() BC,理由如下:
BC,理由如下:
过点C作CE⊥CB与MN交于点E,如图2所示:
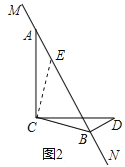
则∠ECB=90
∵∠ACD=90
∴∠ACE=∠DCB
∵DB⊥AB
∴∠CAE=∠CDB
∴△ACE≌△DCB(ASA)
∴AE=DB,EC=BC
∴EB=ABAE=ABDB,△ECB为等腰直角三角形,
∴EB=![]() BC
BC
∴ABBD=![]() BC.
BC.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC在平面直角坐标系中的位置如图所示,
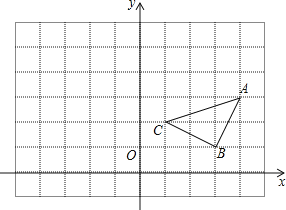
(1)写出△ABC三个顶点的坐标;
(2)求出△ABC的面积;
(3)在图中画出把△ABC先向左平移5个单位,再向上平移2个单位后所得的△A′B′C′,并写出各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+800.
(1)该商店每月的利润为W元,写出利润W与销售单价x的函数关系式;
(2)若要使每月的利润为20000元,销售单价应定为多少元?
(3)商店要求销售单价不低于280元,也不高于350元,求该商店每月的最高利润和最低利润分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数![]() 的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和![]() 的表达式;
的表达式;
(2)已知点C(0,10),试在该一次函数图象上确定一点M,使得MB=MC。求此时点M的坐标.
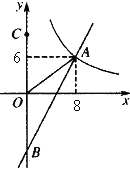
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的序号是________.
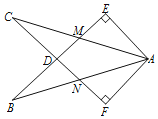
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是多项式
是多项式![]() 的常数项,
的常数项,![]() 是项数.
是项数.
(1)![]() ;
;![]() ;
;
(2)在数轴上,点![]() 、
、![]() 分别对应实数
分别对应实数![]() 和
和![]() ,点
,点![]() 到点
到点![]() 和点
和点![]() 的距离分别为
的距离分别为![]() 和
和![]() ,且
,且![]() ,试求点
,试求点![]() 对应的实数.
对应的实数.
(3)动点M从A点出发,以每秒1个单位长度的速度沿数轴向右运动;动点N从B点以每秒3个单位长度的速度向左匀速运动,到达A点后,立即改变方向往右运动到达B点后停止运动;若M、N同时出发,在此过程中,经过多少秒时点N为MB或MA的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用相同的小立方体搭一个几何体,从正面、上面看到的形状图如图所示,从上面看到的形状图中小正方形的字母表示在该位置上小立方体的个数,请回答下列问题:
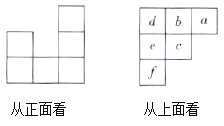
(1)a,b,c各表示的数字是几?
(2)这个几何体最多由几个小立方体搭成?最少呢?
(3)当![]() ,
,![]() 时,画出这个几何体从左面看得到的形状图.
时,画出这个几何体从左面看得到的形状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
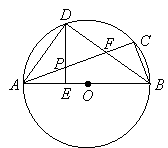
【1】求证:∠DAC =∠DBA;
【2】求证:![]() 是线段AF的中点
是线段AF的中点
【3】若⊙O 的半径为5,AF = ![]() ,求tan∠ABF的值.
,求tan∠ABF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com