【题目】如图，已知△ABC在平面直角坐标系中的位置如图所示，
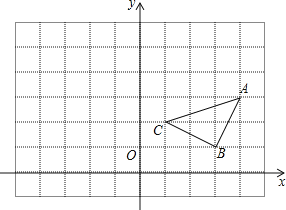
（1）写出△ABC三个顶点的坐标；
（2）求出△ABC的面积；
（3）在图中画出把△ABC先向左平移5个单位，再向上平移2个单位后所得的△A′B′C′，并写出各顶点坐标．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在数轴上，表示数x的点到原点的距离用|x|表示，如果表示数m的点和﹣5的点之间的距离是3，那么m=_____；|c﹣
|+|c﹣4|+|c+1|的最小值是_____
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某县对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．
请根据图表信息回答下列问题：
（1）样本容量为 ；
（2）在频数分布表中，a= ，b= ，并将频数分布直方图补充完整；
（3）若视力在 4.6 以上（含 4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个正方体的六个面上分别标有﹣1，﹣2，﹣3，﹣4，﹣5，﹣6中的一个数，各个面上所标数字都不相同，如图是这个正方体的三种放置方法，三个正方体下底面所标数字分别是a，b，c，则a+b+c+abc＝_____．
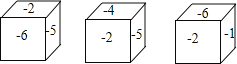
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，一个正方体纸盒的棱长为6厘米，则它的表面积为 平方厘米．
（2）将该正方体的一些棱剪开展成一个平面图形，则需要剪卉 条棱，并求这个平面图形的周长．
（3）如图2，一个长方体纸盒的长、宽、高分别是a厘米、b厘米、c厘米（a＞b＞c）将它的一些棱剪开展成一个平面图形，求这个平面图形的最大周长，画出周长最大的平面图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数学拓展课上，九（1）班同学根据学习函数的经验，对新函数y=x2﹣2|x|的图象和性质进行了探究，探究过程如下：
【初步尝试】求二次函数y=x2﹣2x的顶点坐标及与x轴的交点坐标；
【类比探究】当函数y=x2﹣2|x|时，自变量x的取值范围是全体实数，下表为y与x的几组对应值．
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
①根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请你画出该函数图象的另一部分；
②根据画出的函数图象，写出该函数的两条性质．
【深入探究】若点M（m，y1）在图象上，且y1≤0，若点N（m+k，y2）也在图象上，且满足y2≥3恒成立，求k的取值范围．
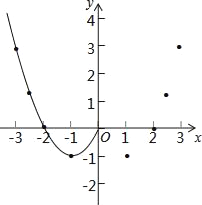
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于平面直角坐标系xOy中的点和⊙O，给出如下定义：过点A的直线l交⊙O于B，C两点，且A、B、C三点不重合，若在A、B、C三点中，存在位于中间的点恰为以另外两点为端点线段的中点时，则称点A为⊙O的价值点．
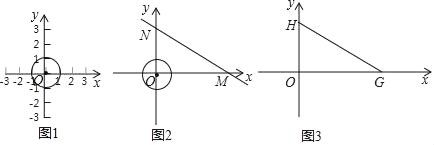
（1）如图1，当⊙O的半径为1时．
①分别判断在点D（
，），E（﹣1，
），F（2，3）中，是⊙O的价值点有 ；
②若点P是⊙O的价值点，点P的坐标为（x，0），且x＞0，则x的最大值为 ．
（2）如图2，直线y=﹣
x+3与x轴，y轴分别交于M、N两点，⊙O半径为1，直线MN上是否存在⊙O的价值点？若存在，求出这些点的横坐标的取值范围，若不存在，请说明理由；
（3）如图3，直线y=﹣x+2与x轴、y轴分别交于G、H两点，⊙C的半径为1，且⊙C在x轴上滑动，若线段GH上存在⊙C的价值点P，求出圆心C的横坐标的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算：
（1）﹣3.25﹣（﹣19）+（﹣6.75）+179
（2）116﹣（﹣40+100）+2（15﹣27）
（3）（﹣9）÷（
）×（
）
（4）﹣14+16÷（﹣2）3×|﹣3﹣1|﹣1
查看答案和解析>>
科目：初中数学 来源： 题型：
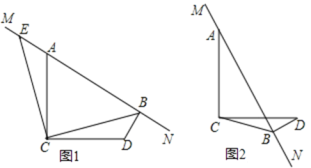
【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC．
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA．
①求证：点E在直线MN上；
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想．
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
