
【题目】(1)如图1,一个正方体纸盒的棱长为6厘米,则它的表面积为 平方厘米.

(2)将该正方体的一些棱剪开展成一个平面图形,则需要剪卉 条棱,并求这个平面图形的周长.
(3)如图2,一个长方体纸盒的长、宽、高分别是a厘米、b厘米、c厘米(a>b>c)将它的一些棱剪开展成一个平面图形,求这个平面图形的最大周长,画出周长最大的平面图形.
【答案】(1)216;(2)7;(3)8a+4b+2c.
【解析】
(1)根据正方体表面积公式即可求解;
(2)①根据正方体的棱的条数以及展开后平面之间应有棱连着,可得出正方体表面展开要剪开的棱的条数;剪开1条棱,增加两个正方形的边长,依此即可求解.
②根据边长最长的都剪,边长最短的减的最少,可得答案
解:(1)正方体的表面积=6×62=216cm2.
故答案为216.
(2)∵正方体有6个表面,12条棱,要展成一个平面图形必须5条棱连接,
∴要剪12﹣5=7条棱,
4×(7×2)
=4×14
=56(cm).
∴这个平面图形的周长是56cm;
故答案为7.
(3)如图:
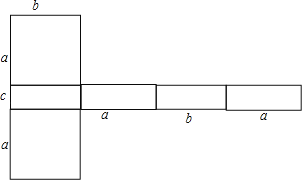 ,
,
这个平面图形的最大周长是8a+4b+2c.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】一个正五边形与一个正方形的边长正好相等,在它们相接的地方,形成一个完整的“苹果”图案(如图).如果让正方形沿着正五边形的四周滚动,并且始终保持正方形和正五边形有两条边邻接,那么第一次恢复“苹果”的图形时,正方形要绕五边形转( )圈.
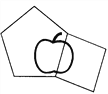
A. 4 B. 3 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把![]() 叫做P1、P2两点间的直角距离,记作d(P1,P2).
叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(2)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.试求点M(2,1)到直线y=x+2的直角距离.
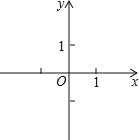
查看答案和解析>>
科目:初中数学 来源: 题型:
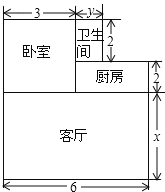
【题目】小张准备购买一套新房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
(1)写出用含x、y的代数式表示的地面总面积;
(2)若x=5,y=1.5,铺设1m2地砖的平均费用为180元,则铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC在平面直角坐标系中的位置如图所示,
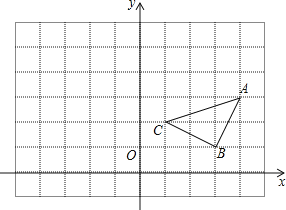
(1)写出△ABC三个顶点的坐标;
(2)求出△ABC的面积;
(3)在图中画出把△ABC先向左平移5个单位,再向上平移2个单位后所得的△A′B′C′,并写出各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正方体礼盒如图所示,六个面分别写有“祝”“福”“祖”“国”“万”“岁”,其中“祝”的对面是“祖”,“万”的对面是“岁”,则它的表面展开图可能是( )
A. 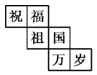 B.
B. 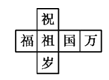 C.
C. 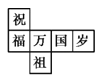 D.
D. 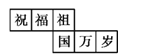
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正三角形纸片剪成四个小正三角形,得到4个小正三角形,称为第一次操作;然后,将其中的一个正三角形再剪成四个小正三角形,共得到7个小正三角形,称为第二次操作;再将其中的一个正三角形再剪成四个小正三角形,共得到10个小正三角形,称为第三次操作;…,根据以上操作,若要得到2014个小正三角形,则需要操作的次数是( )次.
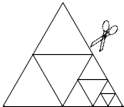
A.669B.670C.671D.672
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的序号是________.
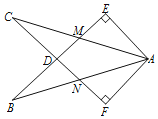
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com