
【题目】已知:如图,ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
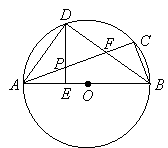
【1】求证:∠DAC =∠DBA;
【2】求证:![]() 是线段AF的中点
是线段AF的中点
【3】若⊙O 的半径为5,AF = ![]() ,求tan∠ABF的值.
,求tan∠ABF的值.
【答案】
【1】∵BD平分∠CBA,∴∠CBD=∠DBA
∵∠DAC与∠CBD都是弧CD所对的圆周角,∴![]() ∠DAC=∠CBD
∠DAC=∠CBD
∴![]() ∠DAC =∠DBA (2分)
∠DAC =∠DBA (2分)
【2】∵AB为直径,∴∠ADB=90°
又∵DE⊥AB于点E,∴∠DEB=90° ∴∠ADE +∠EDB=∠ABD +∠EDB=90°
∴∠ADE=∠ABD=∠DAP
∴PD=PA
又∵∠DFA +∠DAC=∠ADE +∠PD F=90°且∠ADE=∠DAC
∴∠PDF=∠PFD
∴PD=PF ∴PA= PF 即P是线段AF的中点 (3分)
【3】∵∠DAF =∠DBA,∠ADB=∠FDA=90°∴△FDA ∽△ADB
∴![]()
∴在Rt△ABD 中,tan∠ABD= ,即tan∠ABF=
,即tan∠ABF=![]() (3分)
(3分)
【解析】(1)根据圆周角定理得出∠DAC=∠CBD,以及∠CBD=∠DBA得出答案即可;
(2)首先得出∠ADB=90,再根据∠DFA+∠DAC=∠ADE+∠PDF=90°,且∠ADB=90°得出∠PDF=∠PFD,从而得出PA=PF;
(3)利用相似三角形的判定得出△FDA∽△ADB即可得出答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣3.25﹣(﹣19)+(﹣6.75)+179
(2)116﹣(﹣40+100)+2(15﹣27)
(3)(﹣9)÷(![]() )×(
)×(![]() )
)
(4)﹣14+16÷(﹣2)3×|﹣3﹣1|﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
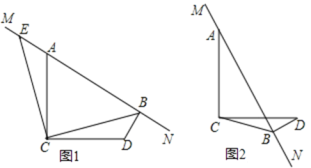
【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC.
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA.
①求证:点E在直线MN上;
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想.
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学附近的文具用品商店最近新进了一批涂卡笔,每支8元,为了合理定价,在第一周试行机动价格,卖出时每支以10元为标准,超出10元的部分记为正,不足10元的部分记为负,文具店售货员记录了第一周涂卡笔的售价情况和售出情况:
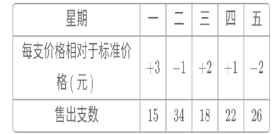
(1)这一周文具用品店的涂卡笔哪天售出的单价最高?最高单价是多少元?
(2)这一周文具用品店出售此种涂卡笔的收益如何?(盈利或亏损的钱数)
(3)文具用品店为了促销这种涂卡笔,决定从下周一起推出两种促销方式:
方式一:购买不超过3支涂卡笔,每支12元,超出3支的部分,每支打九折;
方式二:每支售价12元,购买一支涂卡笔就赠送成本价为0.8元的矿泉水一瓶。
有名同学想一次性购买6支涂卡笔,文具店希望该同学通过哪种方式购买才会使文具店盈利较多?请通过计算说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.
(1)直接写出计算结果:2③= ,(-3)④ = ,![]() ⑤= .
⑤= .
(2)计算 24÷23 + (-8)×2③.
查看答案和解析>>
科目:初中数学 来源: 题型:
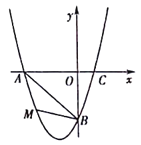
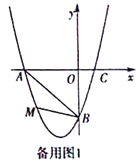
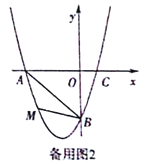
【题目】在平面直角坐标系中,已知抛物线经过A(-3,0),B(0,-3),C(1,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S
关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N(
的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N(![]() ,48)中,在该函数图象上的点有( )
,48)中,在该函数图象上的点有( )
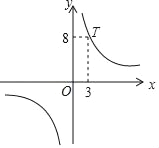
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,如图,点![]() ,点
,点![]() ,连接
,连接![]() ,过点B作直线
,过点B作直线![]() 交
交![]() 于A点,设直线
于A点,设直线![]() 的解析式为
的解析式为![]()
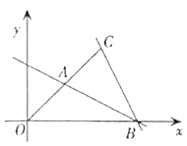
(1)求直线![]() 的函数关系式;
的函数关系式;
(2)若直线![]() 平分
平分![]() 的面积时,求A到x轴的距离;
的面积时,求A到x轴的距离;
(3)作点C关于y轴的对称点D,若直线![]() 与线段
与线段![]() 有交点,求k的取值范围.
有交点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积为
的面积为![]() .
.

(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)若点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,
,![]() 轴,
轴,![]() 轴,垂足分别为点
轴,垂足分别为点![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使得四边形
,使得四边形![]() 为正方形,若存在,请求出点
为正方形,若存在,请求出点![]() 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com