
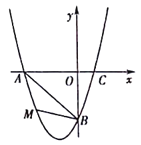
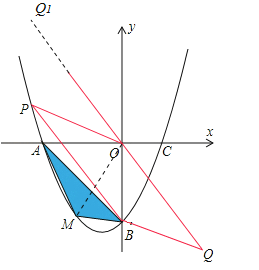
【题目】在平面直角坐标系中,已知抛物线经过A(-3,0),B(0,-3),C(1,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S
关于m的函数关系式,并求出S的最大值;
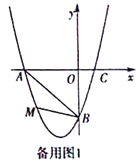
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
【答案】(1)![]()
![]() 时,S最大为
时,S最大为![]()
(3)(-3,3)或![]() 或
或![]() 或(3,-3)
或(3,-3)
【解析】试题分析:(1)先假设出函数解析式,利用三点法求解函数解析式.
(2)设出M点的坐标,利用S=S△AOM+S△OBM﹣S△AOB即可进行解答;
(3)当OB是平行四边形的边时,表示出PQ的长,再根据平行四边形的对边相等列出方程求解即可;当OB是对角线时,由图可知点A与P应该重合,即可得出结论.
试题解析:解:(1)设此抛物线的函数解析式为:y=ax2+bx+c(a≠0),
将A(-3,0),B(0,-3),C(1,0)三点代入函数解析式得: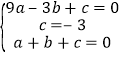
解得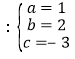 ,所以此函数解析式为:
,所以此函数解析式为:![]() .
.
(2)∵M点的横坐标为m,且点M在这条抛物线上,∴M点的坐标为:(m,![]() ),
),
∴S=S△AOM+S△OBM-S△AOB=![]() ×3×(-
×3×(-![]() )+
)+![]() ×3×(-m)-
×3×(-m)-![]() ×3×3=-(m+
×3×3=-(m+![]() )2+
)2+![]() ,
,
当m=-![]() 时,S有最大值为:S=
时,S有最大值为:S=![]() -.
-.
(3)设P(x,![]() ).分两种情况讨论:
).分两种情况讨论:
①当OB为边时,根据平行四边形的性质知PB∥OQ,
∴Q的横坐标的绝对值等于P的横坐标的绝对值,
又∵直线的解析式为y=-x,则Q(x,-x).
![]() )|=3
)|=3
解得: x=0(不合题意,舍去),-3, ![]() ,∴Q的坐标为(-3,3)或
,∴Q的坐标为(-3,3)或![]() 或
或![]() ;
;
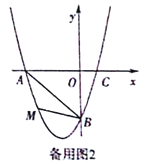
②当BO为对角线时,如图,知A与P应该重合,OP=3.四边形PBQO为平行四边形则BQ=OP=3,Q横坐标为3,代入y=﹣x得出Q为(3,﹣3).
综上所述:Q的坐标为:(-3,3)或![]() 或
或![]() 或(3,-3).
或(3,-3).


科目:初中数学 来源: 题型:
【题目】如图所示,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是多项式
是多项式![]() 的常数项,
的常数项,![]() 是项数.
是项数.
(1)![]() ;
;![]() ;
;
(2)在数轴上,点![]() 、
、![]() 分别对应实数
分别对应实数![]() 和
和![]() ,点
,点![]() 到点
到点![]() 和点
和点![]() 的距离分别为
的距离分别为![]() 和
和![]() ,且
,且![]() ,试求点
,试求点![]() 对应的实数.
对应的实数.
(3)动点M从A点出发,以每秒1个单位长度的速度沿数轴向右运动;动点N从B点以每秒3个单位长度的速度向左匀速运动,到达A点后,立即改变方向往右运动到达B点后停止运动;若M、N同时出发,在此过程中,经过多少秒时点N为MB或MA的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
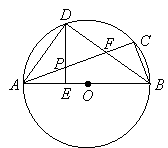
【1】求证:∠DAC =∠DBA;
【2】求证:![]() 是线段AF的中点
是线段AF的中点
【3】若⊙O 的半径为5,AF = ![]() ,求tan∠ABF的值.
,求tan∠ABF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点三角形DEF各顶点的坐标,并求出三角形DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日通过高速公路收费站的汽车中,共有3000辆次缴了通行费,其中大车每辆次缴费20元,小车每辆次缴费10元.设这一天小车缴通行费的辆次为x,总的通行费收入为y元。
(1)试写出y关于x的函数关系式,y是x的一次函数吗?是正比例函数吗?
(2)若小车缴通行费的辆次为1000,这天的通行费收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
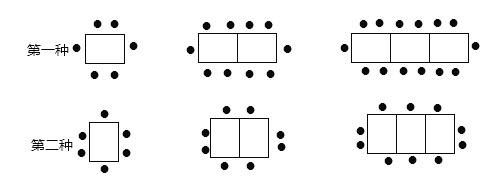
【题目】(9分)某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐___________人;当有![]() 张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
(2)一天中午,餐厅要接待85位顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
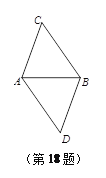
【题目】如图,将线段AB绕点A逆时针旋转α度角得到线段AC,将线段AB绕点B逆时针旋转α度角得到线段BD(0°<α<180°),连结BC、AD.当α=_______度时,四边形ACBD是菱形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com