
【题目】已知![]() 是多项式
是多项式![]() 的常数项,
的常数项,![]() 是项数.
是项数.
(1)![]() ;
;![]() ;
;
(2)在数轴上,点![]() 、
、![]() 分别对应实数
分别对应实数![]() 和
和![]() ,点
,点![]() 到点
到点![]() 和点
和点![]() 的距离分别为
的距离分别为![]() 和
和![]() ,且
,且![]() ,试求点
,试求点![]() 对应的实数.
对应的实数.
(3)动点M从A点出发,以每秒1个单位长度的速度沿数轴向右运动;动点N从B点以每秒3个单位长度的速度向左匀速运动,到达A点后,立即改变方向往右运动到达B点后停止运动;若M、N同时出发,在此过程中,经过多少秒时点N为MB或MA的中点.
【答案】(1)-5;3;(2)-8或6;(3) ![]() 、
、![]() 或
或![]() .
.
【解析】
(1)根据多项式的性质得出a、b即可.
(2)根据绝对值的几何意义,分类讨论.
(3)根据数轴上点运动到不同的位置时,分类讨论.
(1)a=-5,b=3.
(2)由题意得:A表示-5,B表示3,则|AB|=8.

要使得一点P到A的距离和到B的距离为14,则除去AB之间的距离8还差6.
①P点需要距离A点3,距离B点11,则P为-8.
②P点需要距离B点3,距离A点11,则P为6.
故P为:-8或6.
(3)设经过的时间为t秒.N到达A点时t=![]() ,N停止时t=
,N停止时t=![]()
当N未到达A点:M:t-5 N:3-3t
①当N为MB的中点时
B-N=N-M
B+M=2N
3+t-5=2(3-3t) t=![]()
②当N为MA的中点时
M-N=N-A
M+A=2N
t-5+(-5)=2(3-3t) t=![]()
当N到达A点时:M:t-5 N: 3(t-![]() )-5
)-5
③当N为MA中点时
M-N=N-A
M+A=2N
t-5+(-5)=2[3(t-![]() )-5] t=
)-5] t=![]()
④当N为MB中点时
B-N=N-M
B+M=2N
3+(t-5)=2[3(t-![]() )-5] t=
)-5] t=![]() >
>![]() (舍去)
(舍去)
综上所述,经过![]() 、
、![]() 或
或![]() 秒时点N为MB或MA的点.
秒时点N为MB或MA的点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在数学拓展课上,九(1)班同学根据学习函数的经验,对新函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下:
【初步尝试】求二次函数y=x2﹣2x的顶点坐标及与x轴的交点坐标;
【类比探究】当函数y=x2﹣2|x|时,自变量x的取值范围是全体实数,下表为y与x的几组对应值.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
①根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分;
②根据画出的函数图象,写出该函数的两条性质.
【深入探究】若点M(m,y1)在图象上,且y1≤0,若点N(m+k,y2)也在图象上,且满足y2≥3恒成立,求k的取值范围.
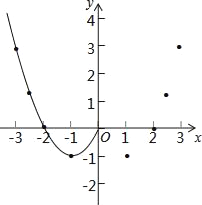
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“泰兴”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了“健康教育”手抄报征集活动,现从中抽取部分作品,按A、B、C、D四个等级进行奖励,并根据统计结果绘制了如下两幅不完整统计图.
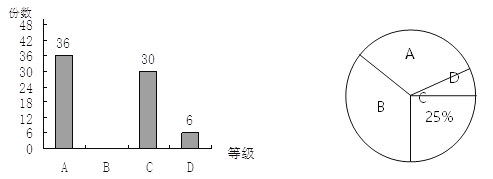
(1)求抽取了多少份作品.
(2)被抽取作品中B等级有多少份?并补全条形统计图.
(3)扇形统计图中D等级所对的圆心角是多少度?
(4)若全校共征集到作品600份,请估计A作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
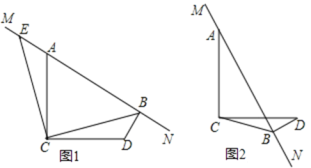
【题目】已知∠ACD=90°,MN是过A点的直线,AC=DC,DB⊥MN于点B,连接BC.
(1)如图1,将△BCD绕点C逆时针方向旋转90°得到△ECA.
①求证:点E在直线MN上;
②猜想线段AB、BD、CB满足怎样的数量关系,并证明你的猜想.
(2)当MN绕点A旋转到如图2的位置时,猜想线段AB、BD、CB又满足怎样的数列关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学附近的文具用品商店最近新进了一批涂卡笔,每支8元,为了合理定价,在第一周试行机动价格,卖出时每支以10元为标准,超出10元的部分记为正,不足10元的部分记为负,文具店售货员记录了第一周涂卡笔的售价情况和售出情况:
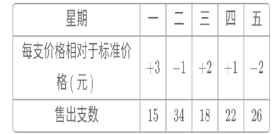
(1)这一周文具用品店的涂卡笔哪天售出的单价最高?最高单价是多少元?
(2)这一周文具用品店出售此种涂卡笔的收益如何?(盈利或亏损的钱数)
(3)文具用品店为了促销这种涂卡笔,决定从下周一起推出两种促销方式:
方式一:购买不超过3支涂卡笔,每支12元,超出3支的部分,每支打九折;
方式二:每支售价12元,购买一支涂卡笔就赠送成本价为0.8元的矿泉水一瓶。
有名同学想一次性购买6支涂卡笔,文具店希望该同学通过哪种方式购买才会使文具店盈利较多?请通过计算说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(-3,0),B(0,-3),C(1,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S
关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
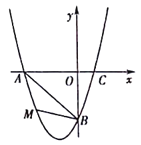
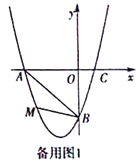
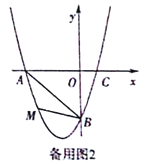
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com