
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“泰兴”的概率.
【答案】(1) ![]() ; (2)
; (2) ![]() .
.
【解析】试题分析:(1)由一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,直接利用概率公式求解即可求得答案;
(2)首先根据题意用表格列举出所有可能的结果与取出的两个球上的汉字恰能组成“美丽”或“泰兴”的情况,再利用概率公式即可求得答案.
试题解析:解:(1)∵有汉字“美”、“丽”、“泰”、“兴”的四个小球,任取一球,共有4种不同结果,∴球上汉字是“美”的概率为P=![]() ;
;
(2)列表如下:
美 | 丽 | 泰 | 兴 | |
美 | ---- | (丽,美) | (泰,美) | (兴,美) |
丽 | (美,丽) | ---- | (泰,丽) | (兴,丽) |
泰 | (美,泰) | (丽,泰) | ---- | (兴,泰) |
兴 | (美,兴) | (丽,兴) | (泰,兴) | ---- |
所有等可能的情况有12种,其中取出的个球上的汉字恰能组成“美丽”或“泰兴”的情况有4种,则P=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
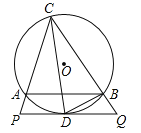
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程![]() 的两实根,且tan∠PCD=
的两实根,且tan∠PCD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
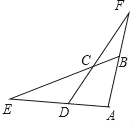
【题目】如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若∠1=![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=﹣2x+800.
(1)该商店每月的利润为W元,写出利润W与销售单价x的函数关系式;
(2)若要使每月的利润为20000元,销售单价应定为多少元?
(3)商店要求销售单价不低于280元,也不高于350元,求该商店每月的最高利润和最低利润分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
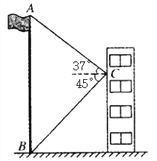
【题目】如图,在教学楼距地面8米高的窗口中C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°.升旗时,国旗上端悬挂在距地面2米处.若国旗随国歌声冉冉升起,并在国歌播放40秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
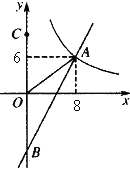
【题目】如图,一次函数y=kx+b的图象分别与反比例函数![]() 的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和![]() 的表达式;
的表达式;
(2)已知点C(0,10),试在该一次函数图象上确定一点M,使得MB=MC。求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是多项式
是多项式![]() 的常数项,
的常数项,![]() 是项数.
是项数.
(1)![]() ;
;![]() ;
;
(2)在数轴上,点![]() 、
、![]() 分别对应实数
分别对应实数![]() 和
和![]() ,点
,点![]() 到点
到点![]() 和点
和点![]() 的距离分别为
的距离分别为![]() 和
和![]() ,且
,且![]() ,试求点
,试求点![]() 对应的实数.
对应的实数.
(3)动点M从A点出发,以每秒1个单位长度的速度沿数轴向右运动;动点N从B点以每秒3个单位长度的速度向左匀速运动,到达A点后,立即改变方向往右运动到达B点后停止运动;若M、N同时出发,在此过程中,经过多少秒时点N为MB或MA的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日通过高速公路收费站的汽车中,共有3000辆次缴了通行费,其中大车每辆次缴费20元,小车每辆次缴费10元.设这一天小车缴通行费的辆次为x,总的通行费收入为y元。
(1)试写出y关于x的函数关系式,y是x的一次函数吗?是正比例函数吗?
(2)若小车缴通行费的辆次为1000,这天的通行费收入是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com