
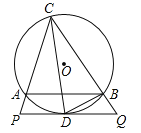
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程![]() 的两实根,且tan∠PCD=
的两实根,且tan∠PCD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)根据平行线的性质和圆周角定理得到∠ABD=∠BDQ=∠ACD,连接OB,OD,交AB于E,根据圆周角定理得到∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,根据三角形的内角和得到2∠ODB+2∠O=180°,于是得到∠ODB+∠O=90°,根据切线的判定定理即可得到结论;
(2)证明:连接AD,根据等腰三角形的判定得到AD=BD,根据相似三角形的性质即可得到结论;
(3)根据题意得到ACBQ=4,得到BD=2,由(1)知PQ是⊙O的切线,由切线的性质得到OD⊥PQ,根据平行线的性质得到OD⊥AB,根据三角函数的定义得到BE=3DE,根据勾股定理得到BE的长,设OB=OD=R,根据勾股定理即可得到结论.
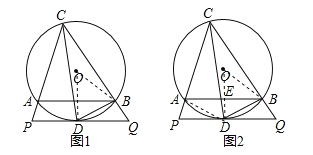
试题解析:(1)证明:∵PQ∥AB,∴∠ABD=∠BDQ=∠ACD,∵∠ACD=∠BCD,∴∠BDQ=∠ACD,如图1,连接OB,OD,交AB于E,则∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,在△OBD中,∠OBD+∠ODB+∠O=180°,∴2∠ODB+2∠O=180°,∴∠ODB+∠O=90°,∴PQ是⊙O的切线;
(2)证明:如图2,连接AD,由(1)知PQ是⊙O的切线,∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD,∴AD=BD,∵∠DBQ=∠ACD,∴△BDQ∽△ACD,∴![]() ,∴BD2=ACBQ;
,∴BD2=ACBQ;
(3)解:方程![]() 可化为x2﹣mx+4=0,∵AC、BQ的长是关于x的方程
可化为x2﹣mx+4=0,∵AC、BQ的长是关于x的方程![]() 的两实根,∴ACBQ=4,由(2)得BD2=ACBQ,∴BD2=4,∴BD=2,由(1)知PQ是⊙O的切线,∴OD⊥PQ,∵PQ∥AB,∴OD⊥AB,由(1)得∠PCD=∠ABD,∵tan∠PCD=
的两实根,∴ACBQ=4,由(2)得BD2=ACBQ,∴BD2=4,∴BD=2,由(1)知PQ是⊙O的切线,∴OD⊥PQ,∵PQ∥AB,∴OD⊥AB,由(1)得∠PCD=∠ABD,∵tan∠PCD=![]() ,∴tan∠ABD=
,∴tan∠ABD=![]() ,∴BE=3DE,∴DE2+(3DE)2=BD2=4,∴DE=
,∴BE=3DE,∴DE2+(3DE)2=BD2=4,∴DE=![]() ,∴BE=
,∴BE=![]() ,设OB=OD=R,∴OE=R﹣
,设OB=OD=R,∴OE=R﹣![]() ,∵OB2=OE2+BE2,∴R2=(R﹣
,∵OB2=OE2+BE2,∴R2=(R﹣![]() )2+(
)2+(![]() )2,解得:R=
)2,解得:R=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】中国企业2016年已经在“一带一路”沿线国家建立了56个经贸合作区,直接为东道国增加了180 000个就业岗位.将180 000用科学记数法表示应为( )
A.18×104
B.1.8×105
C.1.8×106
D.18×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )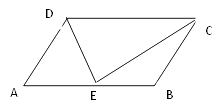
A.96
B.48
C.60
D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
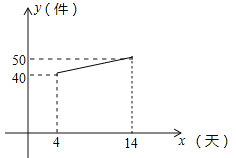
【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系: ![]() .
.
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
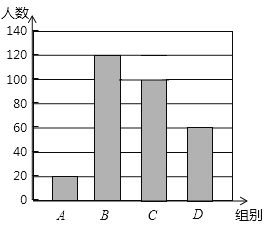
【题目】国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在 组内,中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形三个内角∠A、∠B、∠C,满足关系式∠B+∠C=2∠A,则此三角形( )
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧.若|a-b|=2016,且AO=2BO,则a+b的值为______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
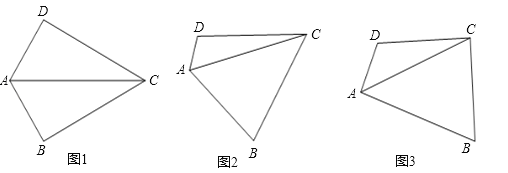
【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.
(2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com