
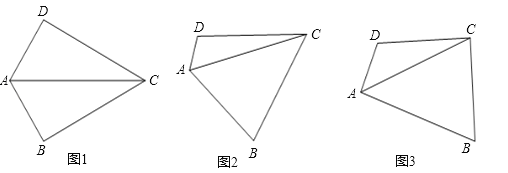
【题目】在四边形ABCD中,∠B+∠D=180°,对角线AC平分∠BAD.
(1)如图1,若∠DAB=120°,且∠B=90°,试探究边AD、AB与对角线AC的数量关系并说明理由.
(2)如图2,若将(1)中的条件“∠B=90°”去掉,(1)中的结论是否成立?请说明理由.
(3)如图3,若∠DAB=90°,探究边AD、AB与对角线AC的数量关系并说明理由.
【答案】(1)AC=AD+AB;(2)成立;(3)AD+AB=![]() AC.
AC.
【解析】
试题分析:(1)结论:AC=AD+AB,只要证明AD=![]() AC,AB=
AC,AB=![]() AC即可解决问题;
AC即可解决问题;
(2)(1)中的结论成立.以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,只要证明△DAC≌△BEC即可解决问题;
(3)结论:AD+AB=![]() AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
AC.过点C作CE⊥AC交AB的延长线于点E,只要证明△ACE是等腰直角三角形,△DAC≌△BEC即可解决问题;
试题解析:(1)AC=AD+AB.
理由如下:如图1中,在四边形ABCD中,∠D+∠B=180°,∠B=90°,∴∠D=90°,∵∠DAB=120°,AC平分∠DAB,∴∠DAC=∠BAC=60°,∵∠B=90°,∴AB=![]() AC,同理AD=
AC,同理AD=![]() AC,∴AC=AD+AB.
AC,∴AC=AD+AB.
(2)(1)中的结论成立,理由如下:以C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,如图2,∵∠BAC=60°,∴△AEC为等边三角形,∴AC=AE=CE,∵∠D+∠B=180°,∠DAB=120°,∴∠DCB=60°,∴∠DCA=∠BCE,∵∠D+∠ABC=180°,∠ABC+∠EBC=180°,∴∠D=∠CBE,∵CA=CB,∴△DAC≌△BEC,∴AD=BE,∴AC=AD+AB.
(3)结论:AD+AB=![]() AC.理由如下:
AC.理由如下:
过点C作CE⊥AC交AB的延长线于点E,如图3,∵∠D+∠B=180°,∠DAB=90°,∴DCB=90°,∵∠ACE=90°,∴∠DCA=∠BCE,又∵AC平分∠DAB,∴∠CAB=45°,∴∠E=45°,∴AC=CE.
又∵∠D+∠B=180°,∠D=∠CBE,∴△CDA≌△CBE,∴AD=BE,∴AD+AB=AE.
在Rt△ACE中,∠CAB=45°,∴AE=![]() =
=![]() AC,∴AD+AB=
AC,∴AD+AB=![]() AC.
AC.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
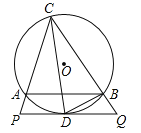
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程![]() 的两实根,且tan∠PCD=
的两实根,且tan∠PCD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中从左到右的变形,是因式分解的是( )
A. (a+2)(a﹣2)=a2﹣4B. x2+x﹣1=(x﹣1)(x+2)+1
C. a+ax+ay=a(x+y)D. a2b﹣ab2=ab(a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
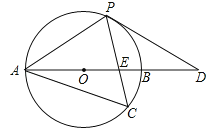
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
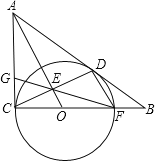
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,甘肃省定西市2018年全市常住人口280.84万人,将数据280.84万用科学记数法表为( )
A. 2.8084×102B. 2.8084×104C. 2.8084×106D. 2.8084×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com