
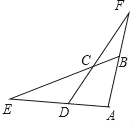
【题目】如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=![]() ,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
,CD=5,CF=ED=n,则AD的长为_____(用含n的式子表示).
【答案】![]()
【解析】分析:作辅助线,构建直角三角形,利用三角函数计算DH和CH的长,并设AD=5a,则DG=3a,AG=4a,证明△AFG∽△CEH,列比例式可得a的值,从而得AD的长.
详解:过C作CH⊥AD于H.
∵cos∠ADC=![]() ,CD=5,∴DH=3,∴CH=4,∴tan∠E=
,CD=5,∴DH=3,∴CH=4,∴tan∠E=![]() =
=![]() ,
,
过A作AG⊥CD于G,设AD=5a,则DG=3a,AG=4a,
∴FG=DF﹣DG=5+n﹣3a.
∵CH⊥AD,AG⊥DF.
∵∠CHE=∠AGF=90°.
∵∠ADC=∠ABC,∴∠EDC=∠CBF.
∵∠DCE=∠BCF,∴∠E=∠F,∴△AFG∽△CEH,
∴![]() ,∴a=
,∴a=![]() ,∴AD=5a=
,∴AD=5a=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
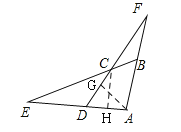
【题目】已知在纸面上有一数轴如图1,根据给出的数轴,解答下面的问题:

(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数.
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A,B的其它字母表示),并写出这些点表示的数.
(4)折叠纸面.若在数轴上﹣1表示的点与5表示的点重合,回答以下问题:
①10表示的点与数 表示的点重合;
②若数轴上M、N两点之间的距离为2018(M在N的左侧),且M、N两点经折叠后重合,求M、N两点表示的数是多少?
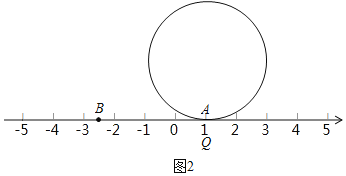
(5)如图2,半径为2的圆周上有一点Q落在数轴上A点处,求将圆在数轴上向右滚动(无滑动)一周后点Q所处的位置的点在数轴上所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
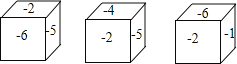
【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学拓展课上,九(1)班同学根据学习函数的经验,对新函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下:
【初步尝试】求二次函数y=x2﹣2x的顶点坐标及与x轴的交点坐标;
【类比探究】当函数y=x2﹣2|x|时,自变量x的取值范围是全体实数,下表为y与x的几组对应值.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
①根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分;
②根据画出的函数图象,写出该函数的两条性质.
【深入探究】若点M(m,y1)在图象上,且y1≤0,若点N(m+k,y2)也在图象上,且满足y2≥3恒成立,求k的取值范围.
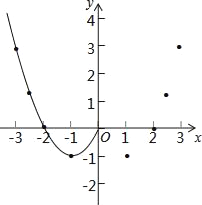
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点和⊙O,给出如下定义:过点A的直线l交⊙O于B,C两点,且A、B、C三点不重合,若在A、B、C三点中,存在位于中间的点恰为以另外两点为端点线段的中点时,则称点A为⊙O的价值点.
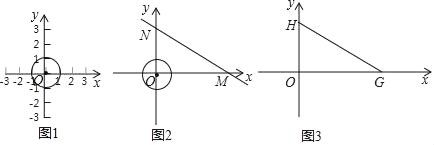
(1)如图1,当⊙O的半径为1时.
①分别判断在点D(![]() ,
,![]() ),E(﹣1,
),E(﹣1,![]() ),F(2,3)中,是⊙O的价值点有 ;
),F(2,3)中,是⊙O的价值点有 ;
②若点P是⊙O的价值点,点P的坐标为(x,0),且x>0,则x的最大值为 .
(2)如图2,直线y=﹣![]() x+3与x轴,y轴分别交于M、N两点,⊙O半径为1,直线MN上是否存在⊙O的价值点?若存在,求出这些点的横坐标的取值范围,若不存在,请说明理由;
x+3与x轴,y轴分别交于M、N两点,⊙O半径为1,直线MN上是否存在⊙O的价值点?若存在,求出这些点的横坐标的取值范围,若不存在,请说明理由;
(3)如图3,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于G、H两点,⊙C的半径为1,且⊙C在x轴上滑动,若线段GH上存在⊙C的价值点P,求出圆心C的横坐标的取值范围.
与x轴、y轴分别交于G、H两点,⊙C的半径为1,且⊙C在x轴上滑动,若线段GH上存在⊙C的价值点P,求出圆心C的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )
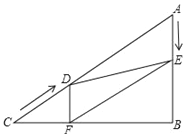
A. 20秒 B. 18秒 C. 12 秒 D. 6秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣3.25﹣(﹣19)+(﹣6.75)+179
(2)116﹣(﹣40+100)+2(15﹣27)
(3)(﹣9)÷(![]() )×(
)×(![]() )
)
(4)﹣14+16÷(﹣2)3×|﹣3﹣1|﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“泰”、“兴”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“泰兴”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学附近的文具用品商店最近新进了一批涂卡笔,每支8元,为了合理定价,在第一周试行机动价格,卖出时每支以10元为标准,超出10元的部分记为正,不足10元的部分记为负,文具店售货员记录了第一周涂卡笔的售价情况和售出情况:
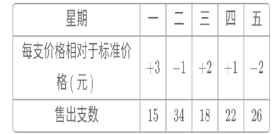
(1)这一周文具用品店的涂卡笔哪天售出的单价最高?最高单价是多少元?
(2)这一周文具用品店出售此种涂卡笔的收益如何?(盈利或亏损的钱数)
(3)文具用品店为了促销这种涂卡笔,决定从下周一起推出两种促销方式:
方式一:购买不超过3支涂卡笔,每支12元,超出3支的部分,每支打九折;
方式二:每支售价12元,购买一支涂卡笔就赠送成本价为0.8元的矿泉水一瓶。
有名同学想一次性购买6支涂卡笔,文具店希望该同学通过哪种方式购买才会使文具店盈利较多?请通过计算说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com