
°æƒø°ø“—÷™‘⁄÷Ω√Ê…œ”–“ª ˝÷·»ÁÕº1£¨∏˘æð∏¯≥ˆµƒ ˝÷·£¨Ω‚¥œ¬√ʵƒŒ £∫

£®1£©«Îƒ„∏˘æðÕº÷–A£¨B¡Ωµ„µƒŒª÷√£¨∑÷±–¥≥ˆÀ¸√«À˘±Ì 浃”–¿Ì ˝£Æ
£®2£©«ÎŒ A£¨B¡Ωµ„÷ƺ‰µƒæý¿Î «∂ý…Ÿ£ø
£®3£©‘⁄ ˝÷·…œª≠≥ˆ”ε„Aµƒæý¿ÎŒ™2µƒµ„£®”√≤ªÕ¨”⁄A£¨Bµƒ∆‰À¸◊÷ƒ∏±Ì 棩£¨≤¢–¥≥ˆ’‚–©µ„±Ì 浃 ˝£Æ
£®4£©’€µ˛÷Ω√ʣƻّ⁄ ˝÷·…œ©Å1±Ì 浃µ„”Î5±Ì 浃µ„÷ÿ∫œ£¨ªÿ¥“‘œ¬Œ £∫
¢Ÿ10±Ì 浃µ„”Î ˝°° °°±Ì 浃µ„÷ÿ∫œ£ª
¢⁄»Ù ˝÷·…œM°¢N¡Ωµ„÷ƺ‰µƒæý¿ÎŒ™2018£®M‘⁄Nµƒ◊Û≤ý£©£¨«“M°¢N¡Ωµ„æ≠’€µ˛∫Û÷ÿ∫œ£¨«ÛM°¢N¡Ωµ„±Ì 浃 ˝ «∂ý…Ÿ£ø
£®5£©»ÁÕº2£¨∞Îæ∂Œ™2µƒ‘≤÷Ð…œ”–“ªµ„Q¬‰‘⁄ ˝÷·…œAµ„¥¶£¨«ÛΩ´‘≤‘⁄ ˝÷·…œœÚ”“πˆ∂Ø£®ŒÞª¨∂Ø£©“ª÷Ð∫Ûµ„QÀ˘¥¶µƒŒª÷√µƒµ„‘⁄ ˝÷·…œÀ˘±Ì 浃 ˝£Æ
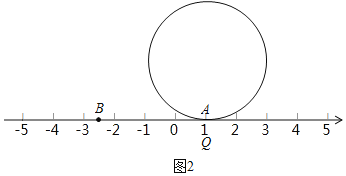
°æ¥∞∏°ø£®1£©A±Ì 浃 ˝ «1£¨B±Ì 浃 ˝ «©Å2.5£ª
£®2£©3.5£ª
£®3£©-1∫Õ3£ª
£®4£©¢Ÿ©Å6£ª¢⁄µ„MŒ™©Å1007£¨µ„NŒ™1011£Æ
£®5£©4¶–+1.
°æΩ‚Œˆ°ø
£®1£© ˝÷·…œ‘≠µ„◊Û≤ýµƒ ˝Œ™∏∫ ˝£¨‘≠µ„”“≤ýµƒ ˝Œ™’˝ ˝£ª
£®2£©A°¢B¡Ωµ„º‰µƒæý¿Îø…±Ì 挙1-£®-2.5£©£¨«ÛΩ‚º¥ø…£ª
£®3£©”ε„Aæý¿ÎŒ™2µƒµ„£¨º¥A◊Û”“¡Ω±þæý¿Î¡Ω∏ˆµ•Œª≥§∂»µƒµ„£¨“≤æÕ « ˝Œ™1©Å2∫Õ1+2µƒµ„£ª
£®4£©¢Ÿœ»«Û≥ˆ-1∫Õ5µƒ÷–µ„£¨‘Ÿ∏˘æð÷––ƒ∂‘≥∆¡– Ωº∆À„º¥ø…µ√Ω‚£ª
¢⁄∏˘æð÷–µ„µƒ∂®“«Û≥ˆMNµƒ“ª∞Σ¨»ª∫Û∑÷±¡– Ωº∆À„º¥ø…µ√Ω‚£ª
£®5£©œ»«Û≥ˆ‘≤µƒ÷Ð≥§£¨‘Ÿ∏˘æð∆Ω“∆πʬ…º¥ø…µ√≥ˆΩ·¬€£Æ
Ω‚£∫£®1£©µ„A±Ì 浃 ˝Œ™1£ªµ„B±Ì 浃 ˝Œ™©Å2.5£ª
£®2£©A°¢B¡Ωµ„÷ƺ‰µƒæý¿ÎŒ™1-£®-2.5£©£Ω3.5£Æ
£®3£©‘⁄ ˝÷·…œª≠≥ˆ”ε„Aµƒæý¿ÎŒ™2µƒµ„∑÷±Œ™3∫Õ©Å1£¨º¥ ˝÷·÷–C∫ÕD£Æ
![]()
£®4£©¢Ÿ£®©Å1+5£©°¬2£Ω2£¨
2©Å£®10©Å2£©£Ω©Å6£Æ
π ¥∞∏Œ™£∫©Å6£ª
¢⁄°þM°¢N¡Ωµ„÷ƺ‰µƒæý¿ÎŒ™2018£¨
°ý![]() MN£Ω
MN£Ω![]() °¡2018£Ω1009£¨
°¡2018£Ω1009£¨
°þ∂‘’€µ„µƒ ˝Œ™2£¨
°ýµ„MŒ™2©Å1009£Ω©Å1007£¨µ„NŒ™2+1009£Ω1011£Æ
£®5£©°þ‘≤µƒ÷Ð≥§=4¶–
°ýΩ´‘≤‘⁄ ˝÷·…œœÚ”“πˆ∂Ø£®ŒÞª¨∂Ø£©“ª÷Ð∫Ûµ„QÀ˘¥¶µƒŒª÷√µƒµ„‘⁄ ˝÷·…œÀ˘±Ì 浃 ˝Œ™4¶–+1£Æ


 ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏
ÃÏÃϜڅœ“ª±æ∫√æÌœµ¡–¥∞∏ –°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
–°—ß…˙10∑÷÷””¶”√Âœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷±œþy£Ωx+b”ÎÀ´«˙œþy£Ω![]() Ωª”⁄µ„A£®©Å1£¨©Å5£©£Æ≤¢∑÷±”Îx÷·°¢y÷·Ωª”⁄µ„C°¢B£Æ
Ωª”⁄µ„A£®©Å1£¨©Å5£©£Æ≤¢∑÷±”Îx÷·°¢y÷·Ωª”⁄µ„C°¢B£Æ

£®1£©÷±Ω”–¥≥ˆb£Ω°° °°£¨m£Ω°° °°£ª
£®2£©∏˘æðÕºœÛ÷±Ω”–¥≥ˆ≤ªµ» Ωx+b£º![]() µƒΩ‚ºØŒ™°° °°£ª
µƒΩ‚ºØŒ™°° °°£ª
£®3£©»Ùµ„D‘⁄x÷·µƒ’˝∞Î÷·…œ£¨ «∑ҥʑ⁄“‘µ„D°¢C°¢Bππ≥…µƒ»˝Ω«–Œ”ΰ˜OABœýÀ∆£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆDµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨…‰œþ![]() …œ”–»˝µ„
…œ”–»˝µ„![]() °¢
°¢![]() °¢
°¢![]() £¨¬˙◊„
£¨¬˙◊„![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨µ„
£¨µ„![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢£¨—ÿ
≥ˆ∑¢£¨—ÿ![]() ∑ΩœÚ“‘
∑ΩœÚ“‘![]() √εƒÀŸ∂»‘»ÀŸ‘À∂Ø£¨µ„
√εƒÀŸ∂»‘»ÀŸ‘À∂Ø£¨µ„![]() ¥”µ„
¥”µ„![]() ≥ˆ∑¢‘⁄œþ∂Œ
≥ˆ∑¢‘⁄œþ∂Œ![]() …œœÚµ„
…œœÚµ„![]() ‘»ÀŸ‘À∂Ø£¨¡Ωµ„Õ¨ ±≥ˆ∑¢£¨µ±µ„
‘»ÀŸ‘À∂Ø£¨¡Ωµ„Õ¨ ±≥ˆ∑¢£¨µ±µ„![]() ‘À∂ØµΩµ„
‘À∂ØµΩµ„![]() ±£¨µ„
±£¨µ„![]() °¢
°¢![]() Õ£÷π‘À∂Ø.
Õ£÷π‘À∂Ø.
(1)»Ùµ„![]() ‘À∂ØÀŸ∂»Œ™
‘À∂ØÀŸ∂»Œ™![]() √Σ¨æ≠π˝∂ý≥§ ±º‰
√Σ¨æ≠π˝∂ý≥§ ±º‰![]() °¢
°¢![]() ¡Ωµ„œý”ˆ?
¡Ωµ„œý”ˆ?
(2)µ±![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ«“
…œ«“![]() ±£¨µ„
±£¨µ„![]() ‘À∂ØµΩµƒŒª÷√«°∫√ «œþ∂Œ
‘À∂ØµΩµƒŒª÷√«°∫√ «œþ∂Œ![]() µƒ»˝µ»∑÷µ„£¨
µƒ»˝µ»∑÷µ„£¨
«Ûµ„![]() µƒ‘À∂ØÀŸ∂»;
µƒ‘À∂ØÀŸ∂»;
(3)µ±µ„![]() ‘À∂ØµΩœþ∂Œ
‘À∂ØµΩœþ∂Œ![]() …œ ±£¨∑÷±»°
…œ ±£¨∑÷±»°![]() ∫Õ
∫Õ![]() µƒ÷–µ„
µƒ÷–µ„![]() °¢
°¢![]() £¨«Û
£¨«Û![]() µƒ÷µ.
µƒ÷µ.
![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø°˜ABC‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–µƒŒª÷√»ÁÕºÀ˘ æ.
£®1£©◊˜≥ˆ°˜ABCπÿ”⁄![]() ÷·∂‘≥∆µƒ°˜A1B1C1£¨≤¢–¥≥ˆ°˜A1B1C1∏˜∂•µ„µƒ◊¯±Í£ª
÷·∂‘≥∆µƒ°˜A1B1C1£¨≤¢–¥≥ˆ°˜A1B1C1∏˜∂•µ„µƒ◊¯±Í£ª
£®2£©Ω´°˜ABCœÚ”“∆Ω“∆6∏ˆµ•Œª£¨◊˜≥ˆ∆Ω“∆∫Ûµƒ°˜A2B2C2£¨≤¢–¥≥ˆ°˜A2B2C2∏˜∂•µ„µƒ◊¯±Í£ª
£®3£©π€≤Ï°˜A1B1C∫Õ°˜A2B2C2£¨À¸√« «∑Òπÿ”⁄ƒ≥÷±œþ∂‘≥∆£ø»Ù «£¨«Î”√ µœþÃıª≠≥ˆ∂‘≥∆÷·°£

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄![]() ÷–£¨∂‘Ω«œþ
÷–£¨∂‘Ω«œþ![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨Ω´π˝µ„
£¨Ω´π˝µ„![]() µƒ÷±œþ
µƒ÷±œþ![]() »∆µ„
»∆µ„![]() –˝◊™£¨Ωª…‰œþ
–˝◊™£¨Ωª…‰œþ![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() .
.
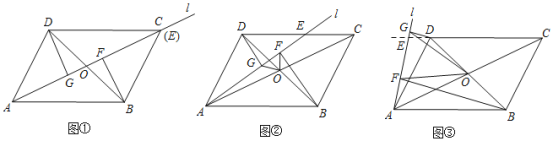
![]() »ÁÕº
»ÁÕº![]() µ±µ„
µ±µ„![]() ”ε„
”ε„![]() ÷ÿ∫œ ±£¨«Î÷±Ω”–¥≥ˆœþ∂Œ
÷ÿ∫œ ±£¨«Î÷±Ω”–¥≥ˆœþ∂Œ![]() µƒ ˝¡øπÿœµ£ª
µƒ ˝¡øπÿœµ£ª
![]() »ÁÕº
»ÁÕº![]() £¨µ±µ„
£¨µ±µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ ±£¨
…œ ±£¨![]() ”Î
”Î![]() ”– ≤√¥ ˝¡øπÿœµ£ø«ÎÀµ√˜ƒ„µƒΩ·¬€£ª
”– ≤√¥ ˝¡øπÿœµ£ø«ÎÀµ√˜ƒ„µƒΩ·¬€£ª
![]() »ÁÕº
»ÁÕº![]() £¨µ±µ„
£¨µ±µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() µƒ—”≥§œþ…œ ±£¨
µƒ—”≥§œþ…œ ±£¨![]() ”Î
”Î![]() ”– ≤√¥ ˝¡øπÿœµ£ø«ÎÀµ√˜ƒ„µƒΩ·¬€.
”– ≤√¥ ˝¡øπÿœµ£ø«ÎÀµ√˜ƒ„µƒΩ·¬€.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡≤¢Ω‚æˆ∆‰∫ÛµƒŒ £∫Œ“√«Ω´Àƒ∏ˆ”–¿Ì ˝![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() –¥≥…
–¥≥…![]()
![]() µƒ–Œ Ω£¨≥∆À¸Œ™”…”–¿Ì ˝
µƒ–Œ Ω£¨≥∆À¸Œ™”…”–¿Ì ˝![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() ◊È≥…µƒ∂˛Ω◊æÿ’Û£¨≥∆
◊È≥…µƒ∂˛Ω◊æÿ’Û£¨≥∆![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Œ™ππ≥…’‚∏ˆæÿ’Ûµƒ‘™Àÿ£¨»Á”…”–¿Ì ˝
Œ™ππ≥…’‚∏ˆæÿ’Ûµƒ‘™Àÿ£¨»Á”…”–¿Ì ˝![]() °¢2°¢3°¢
°¢2°¢3°¢![]() ◊È≥…µƒ∂˛Ω◊æÿ’Û «
◊È≥…µƒ∂˛Ω◊æÿ’Û «![]()
![]() £¨
£¨![]() °¢2°¢3°¢
°¢2°¢3°¢![]() «’‚∏ˆæÿ’Ûµƒ‘™Àÿ£¨µ±«“Ωˆµ±¡Ω∏ˆæÿ’ÛœýÕ¨Œª÷√…œµƒ‘™Àÿœýµ» ±£¨Œ“√«≥∆’‚¡Ω∏ˆ∂˛Ω◊æÿ’Ûœýµ»£¨œ¬√Ê «¡Ω∏ˆ∂˛Ω◊æÿ’Ûµƒº”∑®‘ÀÀ„π˝≥ã∫¢Ÿ
«’‚∏ˆæÿ’Ûµƒ‘™Àÿ£¨µ±«“Ωˆµ±¡Ω∏ˆæÿ’ÛœýÕ¨Œª÷√…œµƒ‘™Àÿœýµ» ±£¨Œ“√«≥∆’‚¡Ω∏ˆ∂˛Ω◊æÿ’Ûœýµ»£¨œ¬√Ê «¡Ω∏ˆ∂˛Ω◊æÿ’Ûµƒº”∑®‘ÀÀ„π˝≥ã∫¢Ÿ![]()
![]() +
+![]()
![]() =
=![]()
![]() =
=![]()
![]() £¨¢⁄
£¨¢⁄![]()
![]() +
+![]()
![]() =
=![]()
![]() =
=![]()
![]() £¨
£¨
£®1£©Õ®π˝π€≤Ï…œ ˆ¿˝◊”÷–æÿ’Ûº”∑®‘ÀÀ„µƒπʬ…£¨ø…πȃ…µ√∂˛Ω◊æÿ’Ûµƒº”∑®‘ÀÀ„∑®‘Ú «£∫¡Ω∏ˆ∂˛Ω◊æÿ’Ûœýº”£¨ .
£®2£©¢Ÿº∆À„£∫![]()
![]() +
+![]()
![]() £ª
£ª
¢⁄»Ù![]()
![]() +
+![]()
![]() =
=![]()
![]() £¨«Û
£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©»Ùº«A=![]()
![]() £¨B=
£¨B=![]()
![]() £¨ ‘“¿æð∂˛Ω◊æÿ’Ûµƒº”∑®∑®‘ÚÀµ√˜A+B=B+A≥…¡¢
£¨ ‘“¿æð∂˛Ω◊æÿ’Ûµƒº”∑®∑®‘ÚÀµ√˜A+B=B+A≥…¡¢
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
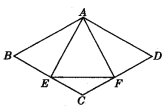
°æƒø°ø“—÷™£∫»ÁÕºÀ˘ 棨¡‚–ŒABCD÷–£¨E£¨F∑÷± «CB£¨CD…œµƒµ„£¨«“BE=DF£Æ
£®1£© ‘Àµ√˜£∫AE=AF£ª
£®2£©»Ù°œB=60°„£¨µ„E£¨F∑÷±Œ™BC∫ÕCDµƒ÷–µ„£¨ ‘Àµ√˜£∫°˜AEFŒ™µ»±þ»˝Ω«–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
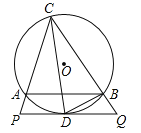
°æƒø°ø»ÁÕº£¨°˜ABCƒ⁄Ω””⁄°—O£¨CD∆Ω∑÷°œACBΩª°—O”⁄D£¨π˝µ„D◊˜PQ°ŒAB∑÷±ΩªCA°¢CB—”≥§œþ”⁄P°¢Q£¨¡¨Ω”BD£Æ
£®1£©«Û÷§£∫PQ «°—Oµƒ«–œþ£ª
£®2£©«Û÷§£∫BD2=ACBQ£ª
£®3£©»ÙAC°¢BQµƒ≥§ «πÿ”⁄xµƒ∑Ω≥Ã![]() µƒ¡Ω µ∏˘£¨«“tan°œPCD=
µƒ¡Ω µ∏˘£¨«“tan°œPCD=![]() £¨«Û°—Oµƒ∞Îæ∂£Æ
£¨«Û°—Oµƒ∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™Àƒ±þ–ŒABCDµƒ“ª◊È∂‘±þAD°¢BCµƒ—”≥§œþœýΩª”⁄µ„E£Æ¡Ì“ª◊È∂‘±þAB°¢DCµƒ—”≥§œþœýΩª”⁄µ„F£¨»Ùcos°œABC=cos°œADC=![]() £¨CD=5£¨CF=ED=n£¨‘ÚADµƒ≥§Œ™_____£®”√∫¨nµƒ Ω◊”±Ì 棩£Æ
£¨CD=5£¨CF=ED=n£¨‘ÚADµƒ≥§Œ™_____£®”√∫¨nµƒ Ω◊”±Ì 棩£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com