
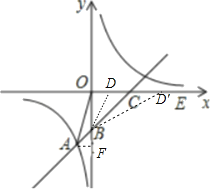
【题目】直线y=x+b与双曲线y=![]() 交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.

(1)直接写出b= ,m= ;
(2)根据图象直接写出不等式x+b<![]() 的解集为 ;
的解集为 ;
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在,请求出D的坐标;若不存在,请说明理由.
【答案】(1)-4,5;(2) x<﹣1或0<x<5;(3)存在,D的坐标是(6,0)或(20,0).
【解析】
(1)把A的坐标分别代入一次函数与反比例函数的解析式,即可求得b和m的值;
(2)根据图象即可直接写出,即反比例函数的图象在一次函数的图象上部的部分x的取值;
(3)求得△OAB的边长,点D在x轴的正半轴上,可以分D在线段OC上(不在O点)或线段OC的延长线上两种情况讨论,依据相似三角形的对应边的比相等即可求得.
解:(1)把A(﹣1,﹣5)代入y=x+b得:﹣5=﹣1+b,解得:b=﹣4.
把A(﹣1,﹣5)代入y=![]() ,得:m=(﹣1)(﹣5)=5.
,得:m=(﹣1)(﹣5)=5.
故答案是:﹣4,5;
(2)解集为:x<﹣1或0<x<5,
故答案是:x<﹣1或0<x<5;
(3)OA=![]() =
=![]() ,
,
在y=x﹣4中,令x=0,解得y=﹣4,则B的坐标是(0,﹣4).
令y=0,解得:x=4,则C的坐标是(4,0).
故OB=4,AB=![]() =
=![]() ,BC=4
,BC=4![]() ,OC=4.
,OC=4.
∴OB=OC,即△OBC是等腰直角三角形,
∴∠OCB=∠OBC=45°,∠BCE=135°.
过A作AF⊥y轴于点F.则△ABF是等腰直角△,∠ABF=45°,∠ABO=135°.
1)当D在线段OC(不与O重合)上时,两个三角形一定不能相似;
2)当D在线段OC的延长线上时,设D的坐标是(x,0),则CD=x﹣4,
∠ABO=∠BCD=135°,
当△AOB∽△DBC时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:x=6,
则D的坐标是(6,0);
当△AOB∽△BDC时,![]() ,即
,即![]() =
=![]() ,
,
解得:x=20,
则D的坐标是(20,0).
则D的坐标是(6,0)或(20,0).


科目:初中数学 来源: 题型:
【题目】数学老师布置了一道思考题“计算(-![]() )÷(
)÷(![]() -
-![]() )”.小明仔细思考了一番,用了一种不同的方法解决了这个问题:原式的倒数为(
)”.小明仔细思考了一番,用了一种不同的方法解决了这个问题:原式的倒数为(![]() -
-![]() )÷(-
)÷(-![]() )=(
)=(![]() -
-![]() )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(-![]() )÷(
)÷(![]() -
-![]() )=
)=![]() .
.
(1)请你通过计算验证小明的解法的正确性.
(2)由此可以得到结论:一个数的倒数的倒数等于_____.
(3)请你运用小明的解法计算:
(-![]() )÷(1
)÷(1![]() -
-![]() -
-![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生到校交通方式情况,随机抽取各年级部分学生就“上下学交通方式”进行问卷调查,调查分为“A:骑自行车;B:步行;C:坐公交车;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图①)和部分扇形统计图(如图②),请根据图中的信息,解答下列问题.
(1)本次调查共抽取 名学生;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)若该中学共有学生3000人,估计有多少学生在上下学交通方式中选择坐公交车?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列各式:
![]() ……试用你发现的规律填空:
……试用你发现的规律填空:![]() ,
,![]() 。
。
(2)请你用含有一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距240km,甲车先从A地出发30min后,乙车从B地出发,相向而行,甲车全程以80km/h的速度行驶,乙车以90km/h的速度行驶1h后,再以75kmh的速度驶完剩余路程,下列选项中能正确反映甲、乙两车距A地的距离y(km)与甲车行驶时间x(h)函数关系的图象是( )
A. 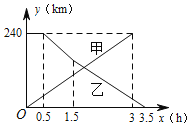 B.
B. 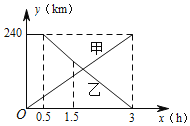
C. 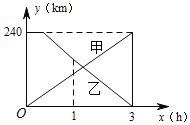 D.
D. 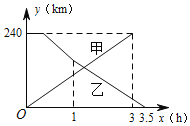
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负.某天自A地出发到收工时所走路线(单位:千米)为:+10,-3,+4,+2,-8,-12,-2,+12,+8,+5.
(1)问收工时距A地多远?
(2)若每千米路程耗油0.2升,问从A地出发到收工共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平圆桌面上有甲乙丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两根相同的管子在容器的5cm高度处连接(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位高度为![]() cm,则开始注入________分钟的水量后,甲与乙的水位高度之差是
cm,则开始注入________分钟的水量后,甲与乙的水位高度之差是![]() cm.
cm.
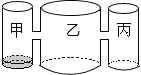
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴如图1,根据给出的数轴,解答下面的问题:

(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数.
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A,B的其它字母表示),并写出这些点表示的数.
(4)折叠纸面.若在数轴上﹣1表示的点与5表示的点重合,回答以下问题:
①10表示的点与数 表示的点重合;
②若数轴上M、N两点之间的距离为2018(M在N的左侧),且M、N两点经折叠后重合,求M、N两点表示的数是多少?
(5)如图2,半径为2的圆周上有一点Q落在数轴上A点处,求将圆在数轴上向右滚动(无滑动)一周后点Q所处的位置的点在数轴上所表示的数.
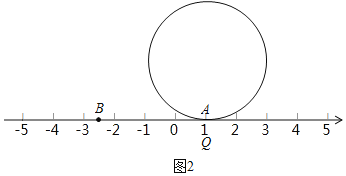
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com