
【题目】(1)观察下列各式:
![]() ……试用你发现的规律填空:
……试用你发现的规律填空:![]() ,
,![]() 。
。
(2)请你用含有一个字母的等式将上面各式呈现的规律表示出来,并用所学数学知识说明你所写式子的正确性。
【答案】(1)192172=4×18,482462=4×47;(2)(n+2)2n2=4(n+1).
【解析】
(1)根据![]() 由6242=4×5,5界于4和6之间的正整数,
由6242=4×5,5界于4和6之间的正整数,![]() ,7界于6和8之间的正整数,11292=4×10,10界于11和9之间的正整数,可得出192172=4×18,482462=4×47;
,7界于6和8之间的正整数,11292=4×10,10界于11和9之间的正整数,可得出192172=4×18,482462=4×47;
(2)由(1)推出该规律为:(n+2)2n2=4(n+1).
(1)根据![]() 由6242=4×5,5界于4和6之间的正整数,
由6242=4×5,5界于4和6之间的正整数,![]() ,7界于6和8之间的正整数,11292=4×10,10界于11和9之间的正整数
,7界于6和8之间的正整数,11292=4×10,10界于11和9之间的正整数
∴可得出192172=4×18,482462=4×47;
(2)由(1)推出该规律为:(n+2)2n2=4(n+1).
故答案为:(1)192172=4×18,482462=4×47;(2)(n+2)2n2=4(n+1).


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
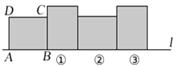
【题目】如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线![]() 上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,...,以此类推,这样连续旋转2018次后,顶点A在整个旋转过程中所经过的路程之和是____________.
上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,...,以此类推,这样连续旋转2018次后,顶点A在整个旋转过程中所经过的路程之和是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们熟知的七巧板,是由宋代黄伯思设计的“燕几图”(“燕几”就是“宴几”,也就是宴请宾客的案几)演变而来.到了明代,严澄将“燕几图”里的方形案几改为三角形,发明了“蝶翅几”.而到了清代初期,在“燕几图”和“蝶翅几”的基础上,兼有三角形、正方形和平行四边形,能拼出更加生动、多样图案的七巧板就问世了(如图1网格中所示)
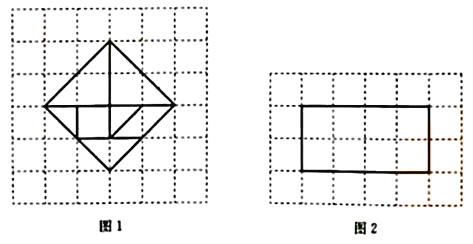
(1)若正方形网格的边长为1,则图1中七巧板的七块拼板的总面积为_____________
(2)使用图1中的七巧板可以拼出一个轮廓如图2所示的长方形,请在图2中画出拼图方法(要求:画出各块拼板的轮廓)
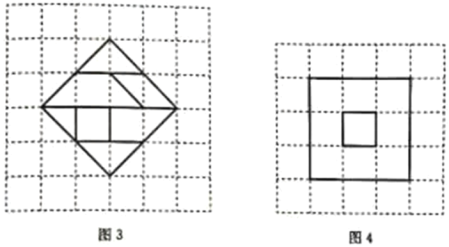
(3)随着七巧板的发展,出现了一些形式不同的七巧板,如图3所示的是另一种七巧板.利用图3中的七巧板可以拼出一个轮廓如图4所示的图形;大正方形的中间去掉一个小正方形,请在图4中画出拼图的方法(要求:画出各块拼板的轮廓)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ΔABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)若E是BD的中点,连结CE,试判断CE与⊙O的位置关系.
(2)若AC=3CD,求∠A的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O是直线AB上一点,OD是∠AOC的平分线,∠COD与∠COE互余
求证:∠AOE与∠COE互补.

请将下面的证明过程补充完整:
证明:∵O是直线AB上一点
∴∠AOB=180°
∵∠COD与∠COE互余
∴∠COD+∠COE=90°
∴∠AOD+∠BOE=_________°
∵OD是∠AOC的平分线
∴∠AOD=∠________(理由:_______________)
∴∠BOE=∠COE(理由:________________)
∵∠AOE+∠BOE=180°
∴∠AOE+∠COE=180°
∴∠AOE与∠COE互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=x+b与双曲线y=![]() 交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.

(1)直接写出b= ,m= ;
(2)根据图象直接写出不等式x+b<![]() 的解集为 ;
的解集为 ;
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在,请求出D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
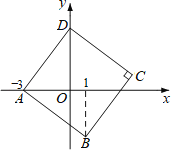
【题目】如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,A(﹣3,0),B(1,b),则正方形ABCD的面积为( )
A.34B.25C.20D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,将过点
,将过点![]() 的直线
的直线![]() 绕点
绕点![]() 旋转,交射线
旋转,交射线![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() 当点
当点![]() 与点
与点![]() 重合时,请直接写出线段
重合时,请直接写出线段![]() 的数量关系;
的数量关系;
![]() 如图
如图![]() ,当点
,当点![]() 在线段
在线段![]() 上时,
上时,![]() 与
与![]() 有什么数量关系?请说明你的结论;
有什么数量关系?请说明你的结论;
![]() 如图
如图![]() ,当点
,当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 有什么数量关系?请说明你的结论.
有什么数量关系?请说明你的结论.
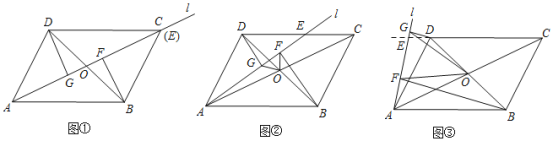
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com