
【题目】矩形ABCD中![]() 平分
平分![]() 交BC于
交BC于![]() 平分
平分![]() 交AD于F.
交AD于F.
(1)说明四边形AECF为平行四边形;
(2)求四边形AECF的面积.
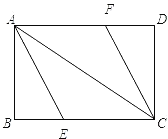
【答案】(1)见解析;(2)30cm2
【解析】试题分析:
(1)由四边形ABCD是矩形可得AD∥BC(即AF∥CE),AB∥CD,由此可得∠BAC=∠ACD,结合AE平分∠BAC,CF平分∠ACD可得∠EAC=∠FCA,即可得到AE∥CF,从而可得四边形AECF是平行四边形;
(2)如图,过点E作EO⊥AC于点O,结合∠B=90°及AE平方∠BAC可得EO=EB,证Rt△ABE≌Rt△AOE可得AO=AB=6,在Rt△ABC中由勾股定理易得AC=10,从而可得OC=4,设CE=x,则EO=BE=BC-CE=8-x,这样在Rt△OEC中由勾股定理建立方程,解方程即可求得CE的值,这样就可求出四边形AECF的面积了.
试题解析:
(1)∵四边形ABCD是矩形,
∴AD∥BC(即AF∥CE),AB∥CD,
∴∠BAC=∠ACD,
又∵AE平分∠BAC,CF平分∠ACD,
∴∠EAC=∠FCA,
∴AE∥CF,
∴四边形AECF是平行四边形;
(2)过点E作EO⊥AC于点O,
∵∠B=90°,AE平分∠BAC,
∴EO=BO,
∵AE=AE,
∴Rt△ABE≌Rt△AOE,
∴AO=AB=6,
∵在Rt△ABC,AC=![]() ,
,
∴OC=AC-AO=4(cm),
设CE=x,则EO=BE=BC-CE=8-x,
∴在Rt△OEC中由勾股定理可得:![]() ,解得:
,解得:![]() ,
,
∴EC=5,
∴S四边形AECF=CE·AB=5×6=30(cm2).



科目:初中数学 来源: 题型:
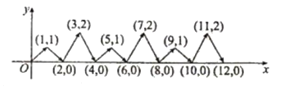
【题目】如图,一个动点P在平面直角坐标系中按箭头所示方向作折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),……,按这样的运动规律,经过第2013次运动后,动点P的坐标是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识再现:已知,如图,四边形ABCD是正方形,点M、N分别在边BC、CD上,连接AM、AN、MN,∠MAN=45°,延长CB至G使BG=DN,连接AG,根据三角形全等的知识,我们可以证明MN=BM+DN.
知识探究:(1)在如图中,作AH⊥MN,垂足为点H,猜想AH与AB有什么数量关系?并证明;
知识应用:(2)如图,已知∠BAC=45°,AD⊥BC于点D,且BD=2,AD=6,则CD的长为 ;
知识拓展:(3)如图,四边形ABCD是正方形,E是边BC的中点,F为边CD上一点,∠FEC=2∠BAE,AB=24,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有__次.

查看答案和解析>>
科目:初中数学 来源: 题型:
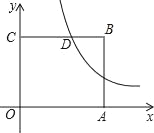
【题目】如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数![]() (x>0,k≠0)的图象经过线段BC的中点D.
(x>0,k≠0)的图象经过线段BC的中点D.
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,高
,高![]() 、
、![]() 相交于点
相交于点![]() ,
, ![]() ,且
,且![]() .
.
(1)求线段 ![]() 的长;
的长;
(2)动点 ![]() 从点
从点 ![]() 出发,沿线段
出发,沿线段 ![]() 以每秒 1 个单位长度的速度向终点
以每秒 1 个单位长度的速度向终点 ![]() 运动,动点
运动,动点 ![]() 从 点
从 点 ![]() 出发沿射线
出发沿射线![]() 以每秒 4 个单位长度的速度运动,
以每秒 4 个单位长度的速度运动,![]() 两点同时出发,当点
两点同时出发,当点 ![]() 到达
到达 ![]() 点时,
点时,![]() 两点同时停止运动.设点
两点同时停止运动.设点 ![]() 的运动时间为
的运动时间为 ![]() 秒,
秒,![]() 的面积为
的面积为 ![]() ,请用含
,请用含![]() 的式子表示
的式子表示 ![]() ,并直接写出相应的
,并直接写出相应的 ![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点 ![]() 是直线
是直线![]() 上的一点且
上的一点且 ![]() .是否存在
.是否存在![]() 值,使以点
值,使以点 ![]() 为顶 点的三角形与以点
为顶 点的三角形与以点 ![]() 为顶点的三角形全等?若存在,请直接写出符合条件的
为顶点的三角形全等?若存在,请直接写出符合条件的 ![]() 值; 若不存在,请说明理由.
值; 若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com