
【题目】如图,菱形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() ,点
,点![]() 为边
为边![]() 的中点.若菱形
的中点.若菱形![]() 的周长为16,
的周长为16,![]() ,则
,则![]() 的面积是______.
的面积是______.
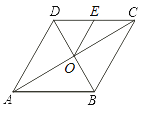
【答案】![]()
【解析】
由菱形的性质四条边相等可求出菱形的边长,结合题干已知条件可求出菱形的面积,则△ADC的面积也可求出,易证OE为△ADC的中位线,所以OE∥AD,再由相似三角形的性质即可求出△OCE的面积.
解:过点D作DH⊥AB于点H,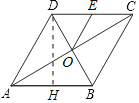
∵四边形ABCD是菱形,
∴AO=CO,AB=BC=CD=AD,
∵菱形ABCD的周长为16,
∴AB=AD=4,
∵∠BAD=60°,
∴DH=4×![]() =2
=2![]() ,
,
∴S菱形ABCD=4×![]() =8
=8![]() ,
,
∴S△CDA=![]() ×8
×8![]() =4
=4![]() ,
,
∵点E为边CD的中点,
∴OE为△ADC的中位线,
∴OE∥AD,OE=2
∴△CEO∽△CDA,
∴△OCE的面积=![]() ×S△CDA=
×S△CDA=![]() ×4
×4![]() =
=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,已知AC=BC=2![]() , AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F.
, AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F.
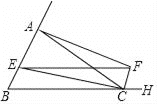
(1)求证:四边形BCFE是平行四边形;
(2)当点E是边AB的中点时,连接AF,试判断四边形AECF的形状,并说明理由;
(3)设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?不存在的,试说明理由;存在的,请直接写出t的值.答:t=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据问题进行证明:
(1)已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P,求证:AP=BQ.
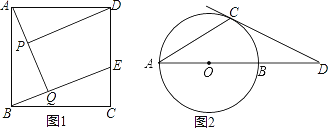
(2)如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D且∠A=∠D.求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
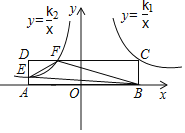
【题目】如图,矩形ABCD的顶点A,B在x轴上,且关于y轴对称,反比例函数y=![]() (x>0)的图象经过点C,反比例函数y=
(x>0)的图象经过点C,反比例函数y=![]() (x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
(x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
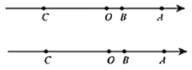
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,
,![]() 是数轴上一点,且
是数轴上一点,且![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,设运动时间为
个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
(1)数轴上点![]() 表示的数为 ,并用含
表示的数为 ,并用含![]() 的代数式表示点
的代数式表示点![]() 所表示的数为 ;
所表示的数为 ;
(2)设![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由,若不变,求线段
的长度是否发生变化?若变化,请说明理由,若不变,求线段![]() 的长度;
的长度;
(3)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向左匀速运动,动点
个单位长度的速度沿数轴向左匀速运动,动点![]() 从点
从点![]() 出发,以点每秒
出发,以点每秒个单位长度沿数轴向左匀速运动,若
![]() 三点同时出发,在运动过程中,
三点同时出发,在运动过程中,![]() 到
到![]() 的距离,
的距离,![]() 到
到![]() 距离中,是否会有这两段距离相等的时候?若有,请求出此时的值;若没有,请说明理由.
距离中,是否会有这两段距离相等的时候?若有,请求出此时的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
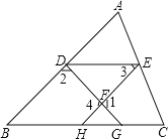
【题目】如图:点D、E、H、G分别在△ABC的边上DE∥BC,∠3=∠B,DG、EH交于点F.求证:∠1+∠2=180°
证明:(请将下面的证明过程补充完整)
∵DE∥BC(已知)
∴∠3=∠EHC(______)
∵∠3=∠B(已知)
∴∠B=∠EHC(______)
∴AB∥EH(______)
∴∠2+∠______=180°(______)
∵∠1=∠4(______)
∴∠1+∠2=180°(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
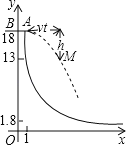
【题目】如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=![]() (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com