
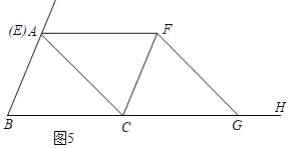
����Ŀ����ͼ��������ABC�У���֪AC��BC��2![]() �� AB��4������ACB�����ƽ����CF����E�ӵ�B��������BA��ÿ��2����λ���ٶ��˶�������E��BC��ƽ���߽�CF�ڵ�F��
�� AB��4������ACB�����ƽ����CF����E�ӵ�B��������BA��ÿ��2����λ���ٶ��˶�������E��BC��ƽ���߽�CF�ڵ�F��
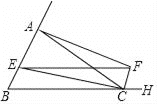
��1����֤���ı���BCFE��ƽ���ı��Σ�
��2������E�DZ�AB���е�ʱ������AF�����ж��ı���AECF����״����˵�����ɣ�
��3�����˶�ʱ��Ϊt�룬�Ƿ����t��ֵ��ʹ������EFC����������Ϊ�ڱ��������ƽ���ı���ǡ�������Σ������ڵģ���˵�����ɣ����ڵģ���ֱ��д��t��ֵ����t��________��
���𰸡���1������������2���ı���AECF�Ǿ��Σ����ɼ���������3��![]() ���5���2��
���5���2��
��������
��1����֪EF��BC�������֪������������Ա߷ֱ�ƽ��֤��BCFE��ƽ���ı��Σ���ΪAC=BC���ȽǶԵȱߣ��á�B����BAC��CFƽ�֡�ACH�����ACF����FCH����ϡ�ACH����B+��BAC����ACF+��FCH�����������á�FCH����B����ͬλ�������ֱ��ƽ�У���BE��CF�����EF��BC��֤���ı���BCFE��ƽ���ı��Σ�
��2����֤��AED=90������֤�ı���AECF��ƽ���ı��Σ����ı���AECF��ƽ���ı����Ǿ��Σ�AC��BC��E��AB���е㣬�ɵ������������ߺ�һ����֪CE��AB����Ϊ�ı���BCFE��ƽ���ı��Σ���CF��BE��AE��AE��CF��һ��Ա�ƽ������ȣ�����һ�ڽ���ֱ�ǣ����ı���AECF�Ǿ��Σ�
��3��������������Т���EF��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ�����ڱ�BE=BC����ʱ����S=vt=2t=![]() , ���t���ɣ�����CE��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����C��CD��AB��D��AC=BC�����ߺ�һ��BD�ij�������Rt��BDC�����ù��ɶ������CD�ij�����ED���ú�t�Ĵ���ʽ��ʾ��������֪EG=CF=EC=EB=2t����Rt��EDC�У����ù��ɶ�����ʽ�������t������CE��EF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����CA��AF��BC����ʱE��A�غϣ���2t=AB=4, ���tֵ����.
, ���t���ɣ�����CE��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����C��CD��AB��D��AC=BC�����ߺ�һ��BD�ij�������Rt��BDC�����ù��ɶ������CD�ij�����ED���ú�t�Ĵ���ʽ��ʾ��������֪EG=CF=EC=EB=2t����Rt��EDC�У����ù��ɶ�����ʽ�������t������CE��EF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����CA��AF��BC����ʱE��A�غϣ���2t=AB=4, ���tֵ����.
��1��֤������ͼ1����AC��BC��
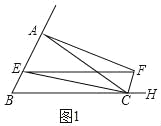
���B����BAC��
��CFƽ�֡�ACH��
���ACF����FCH��
�ߡ�ACH����B+��BAC����ACF+��FCH��
���FCH����B��
��BE��CF��
��EF��BC��
���ı���BCFE��ƽ���ı���
��2���⣺�ı���AECF�Ǿ��Σ������ǣ�
��ͼ2����E��AB���е㣬AC��BC��
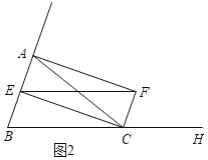
��CE��AB��
���AEC��90����
�ɣ�1��֪���ı���BCFE��ƽ���ı��Σ�
��CF��BE��AE��
��AE��CF��
���ı���AECF�Ǿ���
��3��![]() ���5���2��
���5���2��
�����������
����EF��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ3��
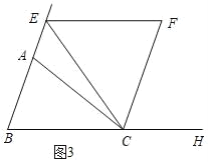
��BE��BC����2t��2 ![]() ��
��
t�� ![]() ��
��
����CE��CF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ4����C��CD��AB��D��

��AC��BC��AB��4��
��BD��2��
�ɹ��ɶ����ã�CD�� ![]() ��
�� ![]() ��6��
��6��
��EG2��EC2 �� ����2t��2��62+��2t��2��2 ��
t��5��
����CE��EF����Ϊ�ڱ��������ƽ���ı���ǡ��������ʱ����ͼ5��CA��AF��BC����ʱE��A�غϣ�
��t��2��
���ϣ�t��ֵΪ![]() ���5���2�룻
���5���2�룻
�ʴ�Ϊ�� ![]() ���5���2�룮
���5���2�룮


 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��4��0����B��0��3����C��4��3����I����ABC�����ģ�����ABC��ԭ����ʱ����ת90����I�Ķ�Ӧ��I'������Ϊ��������
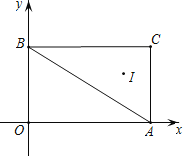
A. ����2��3�� B. ����3��2�� C. ��3����2�� D. ��2����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
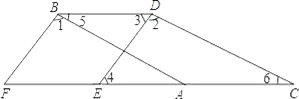
����Ŀ����ͼ����֪��1=��2����3=��4����5=��6�����ж�ED��FB��λ�ù�ϵ����˵��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
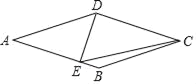
����Ŀ����ͼ������ABCD�У�DE��AB������Ϊ��E������CE����AE��2����DCE��30���������εı߳�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУҪ��С�졢С����С������ͬѧ����ѡһ��ͬѧ�μ���ѧ������������������Ĵ�ר������У��������˵ijɼ����±���ʾ��
ѧ�� ר�� | ����֤�� | PISA���� | Ӧ���� | �������� |
�� | 70 | 75 | 80 | 85 |
�� | 80 | 80 | 72 | 76 |
�� | 75 | 75 | 90 | 65 |
��1�������С���ƽ����Ϊ���٣�
��2����У�����Ĵ�ר�⿼�Գɼ�����Ҫ�̶Ȳ�ͬ������ÿ��ר��ɼ�һ��Ȩ�أ�Ȩ�ر�����Ϊx��1��2��1�����ó����˵ijɼ�����Ȩƽ�����������Ӹ߷ֵ��ͷ�����ΪС����С����С�죬��������x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y=��2x+2��ͼ��ֱ���x�ᣬy�ύ��A��B���㣬��C�ڵ�һ���ޣ�AC��AB����AC=AB�����C������Ϊ��������
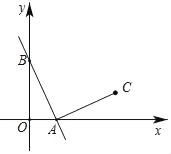
A. ��2��1�� B. ��1��2�� C. ��1��3�� D. ��3��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ�CE��AB���ϵĸߣ�
��1������A=40������B=60�������DCE�Ķ�����
��2������A=m����B=n�����DCE������m��n��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A1(1��0)��A2(1��1)��A3(��1��1)��A4(��1����1)��A5(2����1)���������A2 019������Ϊ____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
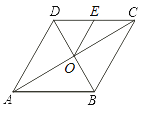
����Ŀ����ͼ������![]() �ĶԽ���
�ĶԽ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
Ϊ��![]() ���е�.������
���е�.������![]() ���ܳ�Ϊ16��
���ܳ�Ϊ16��![]() ����
����![]() �������______��
�������______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com