
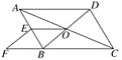
【题目】如图,在ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
(1)求证:四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)首先证明OE是△ABC的中位线,推出OE∥BC,由EF∥OB,即可得出四边形OBFE是平行四边形;
(2)当AD⊥BD时,四边形OBFE是矩形. 只要证明∠EOB=90°即可解决问题.
(1)∵四边形ABCD是平行四边形,
∴点O是AC的中点,
又∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
又∵点F在CB的延长线上,
∴OE∥BF,
∵EF∥BD,即EF∥OB,
∴四边形OBFE是平行四边形;
(2)当AD⊥BD时,四边形OBFE是矩形.
理由:由(1)可知,四边形OBFE是平行四边形,
又∵AD⊥BD,AD∥BC,且点F在BC的延长线上,
∴FC⊥BD,
∴∠OBF=90°,
∴四边形OBFE是矩形.


科目:初中数学 来源: 题型:
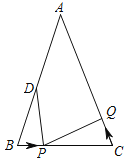
【题目】如图,已知△ABC中,AB=AC=12cm,∠B=∠C,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过多少秒后,点P与点Q第一次在△ABC的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点D,E分别是△ABC的边AB,AC的中点.
(1)如图1,点O是△ABC内的动点,点O,F分别是OB,OC的中点,求证:DEFG是平行四边形;
(2)如图2,若BE交DC于点O,请问AO的延长线经过BC的中点吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )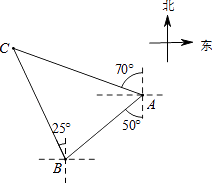
A.10 ![]() 海里
海里
B.10 ![]() 海里
海里
C.10 ![]() 海里
海里
D.20 ![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com