
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.

【答案】(1)详见解析;(2)①详见解析;②:ME=BD,证明详见解析;③∠CNE的度数为7.5°、15°、82.5°、150°.
【解析】
(1)根据中垂线的判定定理“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”可得出结论.
(2)①由∠CAD=15°,BD=AD与直角等腰三角形的性质可知,∠DBA=∠DAB=30°,则可得∠BDE=30°+30°=60°,又根据SSS可证△ADC≌△BDC,则∠ACD=∠BCD=45°,可知∠CDE=∠ACD+∠CAD=45°+15°=60°,故DE平分∠BDC.
②连接MC,由DC=DM,∠CDE=60°,可知△MCD为等边三角形,∠ECM=∠CMD-∠CAD=45°则根据SAS可证△BDC≌△EMC,得出结论ME=BD.
③根据题意可知,分类:当EN=EC时;当EN=CN时;当CE=CN时三种情况求出∠CNE的度数.
(1)证明:∵CB=CA,DB=DA,
∴CD垂直平分线段AB,
∴CD⊥AB,
故答案为:CD⊥AB.
(2)①证明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵在△ADC和△BDC中,
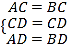 ,
,
∴△ADC≌△BDC(SSS),
∴∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵∠ACB=90°,∠ACD=∠BCD,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠ACD+∠CAD=45°+15°=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
故答案为:DE平分∠BDC.
②结论:ME=BD,
理由:连接MC,

∵DC=DM,∠CDE=60°,
∴△MCD为等边三角形,
∴CM=CD,∠CMD=60°,
又∵EC=CA,∠CAD=15°,
∴∠ECM=∠CMD-∠CAD=45°,
在△BDC和△EMC中,
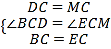 ,
,
∴△BDC≌△EMC(SAS),
∴ME=BD,
故答案为:ME=BD.
③当EN=EC时,∠ENC=7.5°或82.5°;
当EN=CN时,∠ENC=150°;
当CE=CN时,∠CNE=15°,
故答案为:∠CNE的度数为7.5°、15°、82.5°、150°.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题:如图1,△ABC中,∠B=30°,AB=3,BC=4,则△ABC的面积等于
(1)【回顾】
如图1,△ABC中,∠B=30°,AB=3,BC=4,则△ABC的面积等于 . 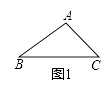
(2)【探究】
图2是同学们熟悉的一副三角尺,一个含有30°的角,较短的直角边长为a;另一个含有45°的角,直角边长为b,小明用两副这样的三角尺拼成一个平行四边形ABCD(如图3),用了两种不同的方法计算它的面积,从而推出sin75°= ![]() ,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°=
,小丽用两副这样的三角尺拼成了一个矩形EFGH(如图4),也推出sin75°= ![]() ,请你写出小明或小丽推出sin75°=
,请你写出小明或小丽推出sin75°= ![]() 的具体说理过程.
的具体说理过程.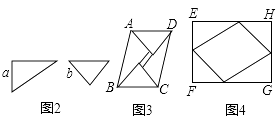
(3)【应用】
在四边形ABCD中,AD∥BC,∠D=75°,BC=6,CD=5,AD=10(如图5)
①点E在AD上,设t=BE+CE,求t2的最小值;
②点F在AB上,将△BCF沿CF翻折,点B落在AD上的点G处,点G是AD的中点吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角的差的绝对值等于![]() ,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,
,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,![]() ,
,![]() ,
,![]() ,则
,则![]() 和
和![]() 互为反余角,其中
互为反余角,其中![]() 是
是![]() 的反余角,
的反余角,![]() 也是
也是![]() 的反余角.
的反余角.
![]() 如图
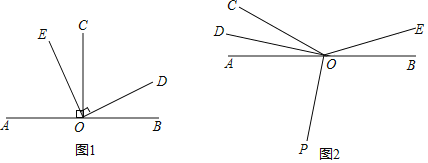
如图![]() 为直线AB上一点,
为直线AB上一点,![]() 于点O,
于点O,![]() 于点O,则
于点O,则![]() 的反余角是______,
的反余角是______,![]() 的反余角是______;
的反余角是______;
![]() 若一个角的反余角等于它的补角的
若一个角的反余角等于它的补角的![]() ,求这个角.
,求这个角.
![]() 如图2,O为直线AB上一点,
如图2,O为直线AB上一点,![]() ,将
,将![]() 绕着点O以每秒
绕着点O以每秒![]() 角的速度逆时针旋转得
角的速度逆时针旋转得![]() ,同时射线OP从射线OA的位置出发绕点O以每秒
,同时射线OP从射线OA的位置出发绕点O以每秒![]() 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,
角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,![]() 与
与![]() 互为反余角
互为反余角![]() 图中所指的角均为小于平角的角
图中所指的角均为小于平角的角![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
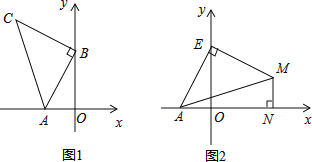
【题目】如图1,![]() ,
,![]() ,以B点为直角顶点在第二象限作等腰直角
,以B点为直角顶点在第二象限作等腰直角![]() .
.
![]() 求C点的坐标;
求C点的坐标;
![]() 在坐标平面内是否存在一点P,使
在坐标平面内是否存在一点P,使![]() 与
与![]() 全等?若存在,直接写出P点坐标,若不存在,请说明理由;
全等?若存在,直接写出P点坐标,若不存在,请说明理由;
![]() 如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角
如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角![]() ,过M作
,过M作![]() 轴于N,直接写出
轴于N,直接写出![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
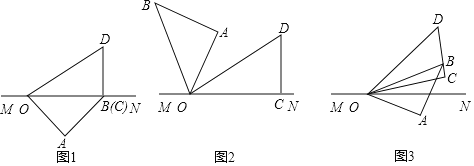
【题目】将一副三角板如图1摆放在直线MN上,在三角板OAB和三角板OCD中,![]() ,
,![]() ,
,![]() .
.
![]() 保持三角板OCD不动,将三角板OAB绕点O以每秒
保持三角板OCD不动,将三角板OAB绕点O以每秒![]() 的速度逆时针旋转,旋转时间为t秒.
的速度逆时针旋转,旋转时间为t秒.
![]() 当
当![]() ______秒时,OB平分
______秒时,OB平分![]() 此时
此时![]() ______
______![]() ;
;
![]() 当三角板OAB旋转至图2的位置,此时
当三角板OAB旋转至图2的位置,此时![]() 与
与![]() 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;
![]() 如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒
如图3,若在三角板OAB开始旋转的同时,另一个三角板OCD也绕点O以每秒![]() 的速度逆时针旋转,当OB旋转至射线OM上时同时停止.
的速度逆时针旋转,当OB旋转至射线OM上时同时停止.
![]() 当t为何值时,OB平分
当t为何值时,OB平分![]() ?
?
![]() 直接写出在旋转过程中,
直接写出在旋转过程中,![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
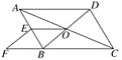
【题目】如图,在ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
(1)求证:四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图![]() 所示放置,图
所示放置,图![]() 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
![]() 请找出图
请找出图![]() 中的全等三角形,并给予说明
中的全等三角形,并给予说明![]() 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母![]() ;
;
![]() 试说明:
试说明:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com