
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
分析 (1)根据表格观察可以得到,下落高度d是弹跳高度b的2倍,从而可以得到哪个选项是正确的;
(2)将d=10代入b=$\frac{d}{2}$,即可解答本题;
(3)将b=100代入b=$\frac{d}{2}$,即可解答本题.
解答 解:(1)由表格可以得到,b=$\frac{d}{2}$,
故选B;
(2)将d=10代入b=$\frac{d}{2}$,得b=5,
即d=10时的弹跳高度b=5;
(3)将b=100代入b=$\frac{d}{2}$,得d=200,
即当弹跳高度b是100时的下落高度d=200.
点评 本题考查一次函数的应用,解题的关键是明确题意,由表格中的数据可以发现其中的函数关系,可以找出所求问题需要的条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
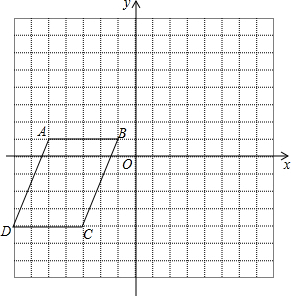 四边形ABCD的顶点坐标分别为A(-5,-1),B(-1,-1),C(-3,-4),D(-7,-4),将四边形ABCD先向上平移5个单位长度,再向右平移8个单位长度.
四边形ABCD的顶点坐标分别为A(-5,-1),B(-1,-1),C(-3,-4),D(-7,-4),将四边形ABCD先向上平移5个单位长度,再向右平移8个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
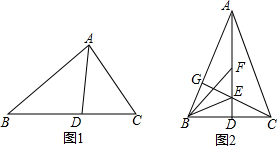
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
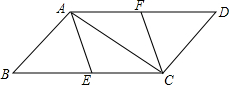 如图,?ABCD中,E,F分别为BC,AD的中点.
如图,?ABCD中,E,F分别为BC,AD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
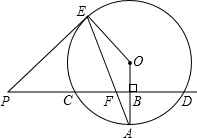 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com