
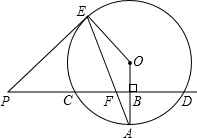
 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.分析 (1)由PE是⊙O的切线,易证得∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,继而可证得∠PEF=∠PFE,根据等角对等边的性质,可得PE=PF;
(2)首先过点P作PG⊥EF于点G,易得∠FPG=∠A,即可得FG=PF•sinA=26×$\frac{5}{13}$=10,又由等腰三角形的性质,求得答案.
解答 解:(1)∵PE是⊙O的切线,
∴∠PEO=90°,
∴∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,
∵OE=OA,
∴∠A=∠AEO,
∴∠PEF=∠PFE,
∴PE=PF;
(2)过点P作PG⊥EF于点G,
∴∠PGF=∠ABF=90°,
∵∠PFG=∠AFB,
∴∠FPG=∠A,
∴FG=PF•sinA=26×$\frac{5}{13}$=10,
∵PE=PF,
∴EF=2FG=20.
点评 此题考查了切线的性质、等腰三角形的判定与性质、圆周角定理、垂径定理、勾股定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
| d | 50 | 80 | 100 | 150 |
| b | 25 | 40 | 50 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com