计算:($\sqrt{24}$-$\sqrt{2}$)-($\sqrt{8}$+$\sqrt{6}$) 题目和参考答案——青夏教育精英家教网—

3．计算：（$\sqrt{24}$-$\sqrt{2}$）-（$\sqrt{8}$+$\sqrt{6}$）

分析先把二次根式化为最简二次根式，再去括号，然后合并同类二次根式，即可得出答案．

解答解：（$\sqrt{24}$-$\sqrt{2}$）-（$\sqrt{8}$+$\sqrt{6}$）
=2$\sqrt{6}$-$\sqrt{2}$-2$\sqrt{2}$-$\sqrt{6}$
=$\sqrt{6}$-3$\sqrt{2}$．

点评此题考查了二次根式的化简求值，在计算时要注意运算顺序和结果的符号，把二次根式化成最简再计算．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

10．

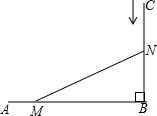如图所示，AB⊥CB，AB=10cm，BC=8cm．一只螳螂由A点以每秒2cm的速度由A向B爬行，与此同时，一口蝉从C点以每秒1cm的速度由C向B爬行，当螳螂和蝉爬行x秒后，它们分别到达了点M，N的位置，此时，△MNB的面积恰好为24cm²．根据题意可得方程（　　）

A．

2x•x=24

B．

（10-2x）（8-x）=24

C．

（10-x）（8-2x）=24

D．

（10-2x）（8-x）=48

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．下表列出了一项试验统计数据，表示将皮球从高处落下时，下落高度d与弹跳高度b的关系：

d	50	80	100	150
b	25	40	50	75

（1）下落高度d与弹跳高度b之间的函数解析式是C
A．b=d²B．b=2d C．b=$\frac{d}{2}$ D．b=d+25
（2）求当d=10时的弹跳高度b；
（3）求当弹跳高度b是100时的下落高度d．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

8．某个正数的两个平方根分别是a-1和3-2a，则实数a的值为（　　）

A．

B．

-$\frac{4}{3}$

C．

D．

-2

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．已知$\sqrt{a-16}$+（b+2）²=0，求$\frac{a}{b}$的立方根．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

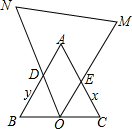如图，△ABC、△OMN均为等边三角形，且O点为BC的中点，△OMN绕着点O旋转，ON、OM分别交BA（BA的延长线），CA（CA的延长线）于D、E两点．
（1）设OB=OC=1，BD=y，CE=x，求y关于x的函数关系式；（不要求写x的取值范围）
（2）在上题中，连结DE，设DE=m，△ODE的面积为s，求s关于m的函数关系式．（不要求写m的取值范围）．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．我校举行春季运动会系列赛中，九年级（1）班、（2）班的竞技实力相当，关于比赛结果，
甲同学说：（1）班与（2）班的得分为6：5；
乙同学说：（1）班的得分比（2）班的得分的2倍少40分；
若设（1）班的得分为x分，（2）班的得分为y分，根据题意所列方程组应为（　　）

A．

$\left\{{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}}\right.$

B．

$\left\{{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}}\right.$

C．

$\left\{{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}}\right.$

D．

$\left\{{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}}\right.$

查看答案和解析>>