
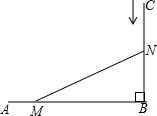
 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )| A. | 2x•x=24 | B. | (10-2x)(8-x)=24 | C. | (10-x)(8-2x)=24 | D. | (10-2x)(8-x)=48 |
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
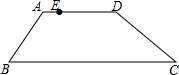 如图,四边形ABCD是梯形,AD∥BC,E为AD上任意一点,∠B+∠C=90°,请先将AB向右平移,使点A与点E重合,交BC于点F,再将CD向作平移,使点D与点E重合,交BC于点G,画出平移后的图形,并判断△EFG的形状.
如图,四边形ABCD是梯形,AD∥BC,E为AD上任意一点,∠B+∠C=90°,请先将AB向右平移,使点A与点E重合,交BC于点F,再将CD向作平移,使点D与点E重合,交BC于点G,画出平移后的图形,并判断△EFG的形状.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com