
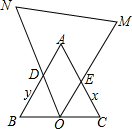
 如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.
如图,△ABC、△OMN均为等边三角形,且O点为BC的中点,△OMN绕着点O旋转,ON、OM分别交BA(BA的延长线),CA(CA的延长线)于D、E两点.分析 (1)只要证明△BOD∽△COE,列出有关比例式子即可.
(2)只要证明△DOE∽△OCE得∠DEO=∠OEC,作OH⊥EC于H,OK⊥DE于K,求出高OK即可解决问题.
解答 解:(1)∵△ABC、△OMN均为等边三角形,
∴∠B=∠C=60°,∠DOE=60°,
∴∠BDO+∠BOD=∠BOD+∠EOC=120°,
∴∠BDO=∠EOC,
∴△BOD∽△COE
∴$\frac{BD}{OC}=\frac{BO}{CE}$,
即$\frac{y}{1}=\frac{1}{x}$,
∴y=$\frac{1}{x}$;
(2)∵△BOD∽△COE,
∴$\frac{DO}{OE}=\frac{BO}{EC}$,
∵BO=CO,
∴$\frac{DO}{CO}=\frac{OE}{EC}$,
∵∠DOE=∠C=60°,
∴△DOE∽△OCE,
∴∠DEO=∠OEC,
作OH⊥EC于H,OK⊥DE于K,
∴OH=OK=$\frac{\sqrt{3}}{2}$,
∴s=$\frac{1}{2}$•m$•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$m.
点评 本题考查等边三角形的性质、相似三角形的判定和性质、三角形的面积等知识,解题的关键是利用相似解决问题,属于中考常考题型.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -1 | -2 | 3 | -0.5 | 1 | 2 | 0.5 |
| y | 3 | 1.5 | -1 | 6 | -3 | -1.5 | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
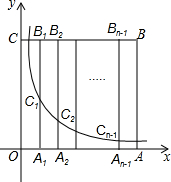 如图,边长为n(n为正整数)的正方形OABC的边OA、OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,B3…,Bn-1为CB的n等分点,连接A1B1,A2B2,A3B3,…,An-1Bn-1,分别与曲线y=$\frac{n-8}{x}$(x>0)相交于点C1,C2,C3…,Cn-1.若B6C6=9A6C6,则n的值是20.
如图,边长为n(n为正整数)的正方形OABC的边OA、OC在坐标轴上,点A1,A2,…,An-1为OA的n等分点,点B1,B2,B3…,Bn-1为CB的n等分点,连接A1B1,A2B2,A3B3,…,An-1Bn-1,分别与曲线y=$\frac{n-8}{x}$(x>0)相交于点C1,C2,C3…,Cn-1.若B6C6=9A6C6,则n的值是20.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
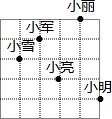 如图,是阳光小区内的一幢商品房示意图,如小军家所在的位置用(2,4)表示.
如图,是阳光小区内的一幢商品房示意图,如小军家所在的位置用(2,4)表示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com