
【题目】已知AB是⊙O的直径,AB=4,点C,点D在⊙O上,CD=2,直线AD,BC交于点E.
(1)如图,若点E在⊙O外,求∠AEB的度数.
(2)若DC∥AB,试求出△ABE的面积.

【答案】(1)60°;(2)4![]() .
.
【解析】
(1)如图1,连接OC、OD,先证明△OCD为等边三角形得到∠COD=60°,利用圆周角定理得到∠CBD=30°,∠ADB=90°,然后利用互余计算出∠AEB的度数;
(2)先证明△OBC为等边三角形,再证明△ABE是等边三角形,然后根据再计算面积即可.
(1)如图1,连接OC、OD,
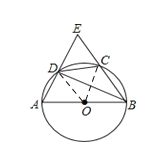
∵CD=2,OC=OD=2,
∴△OCD为等边三角形,
∴∠COD=60°,
∴∠CBD=![]() ∠COD=30°,
∠COD=30°,
∵AB为直径,
∴∠ADB=90°,
∴∠AEB=90°﹣∠DBE=90°﹣30°=60°;
(2)∵DC∥AB,
∴∠OCD=∠DCO=60°,
∴△OBC为等边三角形,
∴∠EBA=60°,
又∵∠AEB=60°,
∴△ABE是等边三角形,
∴AE=AB=BE=4,
∴在Rt△ABD中,![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度![]() (单位:
(单位:![]() )与足球被踢出后经过的时间
)与足球被踢出后经过的时间![]() (单位:
(单位:![]() )之间的关系如下表:
)之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度为![]() ;②足球飞行路线的对称轴是直线
;②足球飞行路线的对称轴是直线![]() ;③足球被踢出
;③足球被踢出![]() 时落地;④足球被踢出
时落地;④足球被踢出![]() 时,距离地面的高度是
时,距离地面的高度是![]() .
.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PE=PA,PE交CD于F.
(1)求证: PC=PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其它条件不变,若∠ABC=65°,则∠CPE=________度.
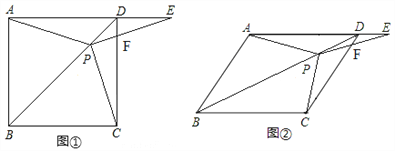
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN.
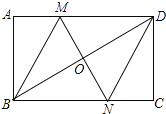
(1)求证:四边形BMDN是菱形;
(2)若AB=2,AD=4,求MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=70°,⊙O切CA、CB分别于点A和点B,则弦AB所对的圆周角的度数为( )
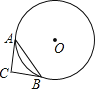
A. 110° B. 55° C. 55°或 110° D. 55 或 125°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
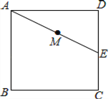
【题目】如图,正方形ABCD的边长为4cm,E为CD边的中点,,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com