
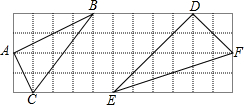
 如图所示,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由.
如图所示,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上,判断△ABC和△DEF是否相似,并说明理由. 分析 首先根据小正方形的边长,求出△ABC和△DEF的三边长,然后判断它们是否对应成比例即可.
解答 解:△ABC和△DEF相似;
理由如下:根据勾股定理,得AB=2$\sqrt{5}$,BC=5,AC=$\sqrt{5}$;DF=2$\sqrt{2}$,DE=4$\sqrt{2}$,EF=2$\sqrt{10}$,
∵$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$=$\frac{\sqrt{10}}{4}$,
∴△ABC∽△DEF.
点评 此题主要考查的是相似三角形的判定方法:如果两个三角形的三组对应边的比相等,那么这两个三角形相似.(SSS)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
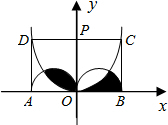 如图,矩形ABCD的长AB=4cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.以AB、OP所在直线为两轴建立直角坐标系,抛物线y=ax2经过C、D两点,则图中阴影部分的面积是$\frac{π}{2}$cm2.
如图,矩形ABCD的长AB=4cm,点O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.以AB、OP所在直线为两轴建立直角坐标系,抛物线y=ax2经过C、D两点,则图中阴影部分的面积是$\frac{π}{2}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 二次函数的图象是抛物线 | |
| B. | 任意一个一元二次方程都有实数根 | |
| C. | 三角形的外心在三角形的外部 | |
| D. | 投掷一枚均匀的硬币100次,正面朝上的次数为50次 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com