
| (2+1)2+(4-0)2 |
| (x-2)2+(4-0)2 |
| (x-2)2+16 |
| (x-2)2+16 |
| (x-2)2+16 |
| 19 |
| 6 |
| 19 |
| 6 |
| 19 |
| 6 |
| 19 |
| 6 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
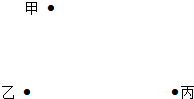 作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)
作图题:如图,现在甲、乙、丙三家公司共建一个污水处理站P,使得该站到乙、丙两家公司的距离相等,且使甲公司到污水处理站P的距离最短,试在图中确定污水处理站P的位置.(要求尺规作图,保留作图痕迹,不写作法,但要写结论)查看答案和解析>>
科目:初中数学 来源: 题型:
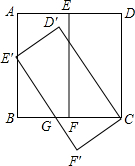 如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G
如图,在正方形ABCD中,点E、F分别是AD、BC中点,连接EF,将矩形CDEF绕着点C逆时针旋转一定角度得到矩形CD′E′F′,点E′恰好落在AB边上,E′F′与BC交于点G 查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com