练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．在Rt△ABC中，∠C=90°，BC=1，那么AB的长为（　　）
    A．sinAB．cosAC．$\frac{1}{cosA}$D．$\frac{1}{sinA}$

    分析 根据在直角三角形中，锐角的正弦为对边比斜边，可得答案．

    解答 解：Rt△ABC中，∠C=90°，BC=1，得
    sinA=$\frac{BC}{AB}$．
    AB=$\frac{BC}{sinA}$=$\frac{1}{sinA}$，
    故选：D．

    点评 本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．如图，在平面直角坐标系xOy中，定义直线x=m与双曲线yn=$\frac{n}{x}$的交点Am，n（m、n为正整数）为“双曲格点”，双曲线yn=$\frac{n}{x}$在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”．

    （1）①“双曲格点”A2，1的坐标为（2，$\frac{1}{2}$）；②若线段A4，3A4，n的长为1个单位长度，则n=7；
    （2）图中的曲线f是双曲线y1=$\frac{1}{x}$的一条“派生曲线”，且经过点A2，3，则f的解析式为y=$\frac{1}{x}$+1；
    （3）画出双曲线y3=$\frac{3}{x}$的“派生曲线”g（g与双曲线y3=$\frac{3}{x}$不重合），使其经过“双曲格点”A2，a、A3，3、A4，b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．为了解学生参加户外活动的情况，某校对初三学生参加户外活动的时间进行抽样调查，并将调查结果绘制成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：
    （1）将条形统计图补画完整．
    （2）求每天参加户外活动时间达到2小时的学生所占调查学生的百分比．
    （3）这批参加调查的初三学生参加户外活动的平均时间是多少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若一个扇形的半径是18cm，且它的弧长是12π cm，则此扇形的圆心角等于（　　）
    A．30°B．60°C．90°D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

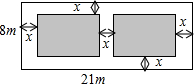    15．某小区有一块长21米，宽8米的矩形空地，如图所示．社区计划在其中修建两块完全相同的矩形绿地，并且两块绿地之间及四周都留有宽度为x米的人行通道．如果这两块绿地的面积之和为60平方米，人行通道的宽度应是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图：在Rt△ABC中，∠C=90°，BC=8，∠B=60°，解直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

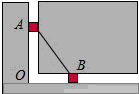    12．图中的两个滑块A，B由一个连杆连接，分别可以在垂直和水平的滑道上滑动．开始时，滑块A距O点20厘米，滑块B距O点15厘米．问：当滑块A向下滑到O点时，滑块B滑动了10厘米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．有这样一个问题：探究函数y=$\frac{1}{x-1}$+x的图象与性质．
    小东根据学习函数的经验，对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究．
    下面是小东的探究过程，请补充完整：
    （1）函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1；
    （2）下表是y与x的几组对应值．
    x…-3-2-10$\frac{1}{2}$$\frac{3}{4}$$\frac{5}{4}$$\frac{3}{2}$2345…
    y…-$\frac{13}{4}$-$\frac{7}{3}$-$\frac{3}{2}$-1-$\frac{3}{2}$-$\frac{13}{4}$$\frac{21}{4}$$\frac{7}{2}$3$\frac{7}{2}$m$\frac{21}{4}$…
    求m的值；
    （3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
    （4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（2，3），结合函数的图象，写出该函数的其它性质（一条即可）：该函数没有最大值，也没有最小值．

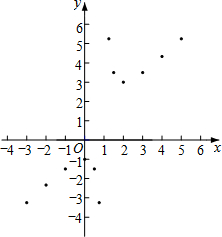
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

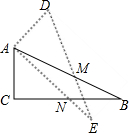    10．如图，在Rt△ABC中，∠C=90°，M为AB边上中点，将Rt△ABC绕点M旋转，使点C与点A重合得Rt△DEA，设AE交CB于点N．
    （1）若∠B=25°，求∠BAE的度数；
    （2）若AC=2，BC=5，求CN的长．

    查看答案和解析>>

    同步练习册答案