
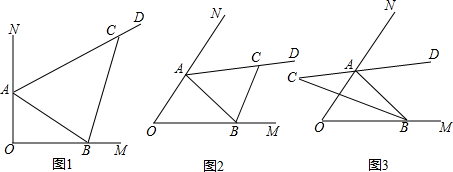
分析 (1)利用外角的性质和三角形的内角和定理可得∠NAB+∠MBA=90°+∠ABO+90°+∠BAO=90°+180°=270°,由角平分线的性质得∠CAB+∠CBA,由内角和定理得∠ACB;
(2)如图1,由角平分线的性质易得∠1=∠2=$\frac{1}{2}$∠BAN,∠3=∠4=$\frac{1}{2}$∠ABM,由三角形外角和定理易得∠2+∠4,得∠ACB;
(3)如图2,同(2)可得结论.
解答 解:(1)∵∠MON=90°,∠NAB=∠AOB+∠ABO=90°+∠ABO,∠ABM=∠AOB+∠BAO=90°+∠BAO,
∴∠NAB+∠MBA=90°+∠ABO+90°+∠BAO=90°+180°=270°,
∵AD平分∠BAN,BC平分∠ABM,
∴∠CAB+∠CBA=$\frac{1}{2}×270°$=135°,
∴∠ACB=45°;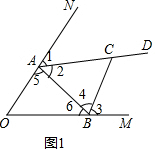
(2)∠ACB的度数不改变
如图1,∵AD平分∠BAN,BC平分∠ABM,
∴∠1=∠2=$\frac{1}{2}$∠BAN,∠3=∠4=$\frac{1}{2}$∠ABM,
∵∠BAN=∠O+∠6,∠ABM=∠O+∠5,
∴∠2+∠4=$\frac{1}{2}$(∠BAN+∠ABM)=$\frac{1}{2}$(∠O+∠5+∠O+∠6)=90°+$\frac{1}{2}$∠O,
∴∠ACB=180°-(∠2+∠4)=90°-$\frac{1}{2}$∠O=90°-$\frac{1}{2}$α;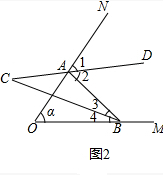
(3)∠ACB的度数不改变,
如图2,∵∠2=∠ACB+∠3,∠NAB=α+∠3+∠4,AD平分∠BAN,BC平分∠ABO,
∴∠NAB=2∠2,
∴2∠2=α+2∠3,
∴∠2=$\frac{1}{2}α$+∠3,
∴∠ACB=$\frac{1}{2}$α.
点评 本题主要考查了角平分线的性质,外角性质和三角形的内角和定理,综合运用各定理是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
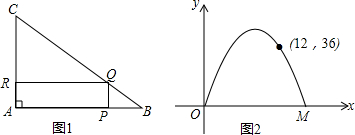
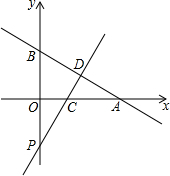 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的图象与坐标轴分别交于点A和B两点,将△AOB沿直线CD折起,使点A与点B重合,直线CD交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com