
【题目】如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 . 
【答案】![]() π
π
【解析】解:如图点P运动的路径是以G为圆心的弧 ![]() ,在⊙G上取一点H,连接EH、FH.
,在⊙G上取一点H,连接EH、FH.
∵四边形AOCB是正方形,
∴∠AOC=90°,
∴∠AFP= ![]() ∠AOC=45°,
∠AOC=45°,
∵EF是⊙O直径,
∴∠EAF=90°,
∴∠APF=∠AFP=45°,
∴∠H=∠APF=45°,
∴∠EGF=2∠H=90°,
∵EF=4,GE=GF,
∴EG=GF=2 ![]() ,
,
∴ ![]() 的长=
的长= ![]() =
= ![]() π.
π.
所以答案是 ![]() π.
π.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6 ![]() ,则FG的长为 .
,则FG的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) 
A.π
B.![]()
C.3+π
D.8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,四边形ABCD中AB∥CD,AB≠CD,BD=AC。
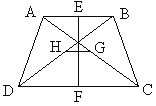
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42-x)名工人生产圆形铁片,则下列所列方程正确的是( )
A. 120x=2×80(42-x) B. 80x=120(42-x)
C. 2×80x=120(42-x) D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com