
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,垂足为点
,垂足为点![]() ,连结
,连结![]() 、
、![]() .
.
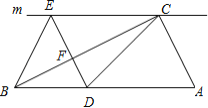
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若点![]() 是
是![]() 中点,当四边形
中点,当四边形![]() 是正方形时,则
是正方形时,则![]() 大小满足什么条件?
大小满足什么条件?
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
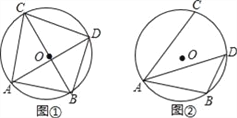
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点;
的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
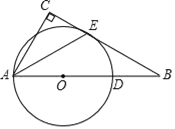
【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成推理过程.
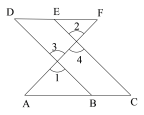
如图,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
证明:∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴∠2=∠3( )
∴____∥______( )
∴∠C=∠ABD( )
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料并填空:
①(1﹣![]() )(1+
)(1+![]() )=1﹣
)=1﹣![]() ,反过来,得1﹣
,反过来,得1﹣![]() =(1﹣
=(1﹣![]() )(1+
)(1+![]() )=
)=![]() ×
×![]() ;
;
②(1﹣![]() )(1+
)(1+![]() )=1﹣
)=1﹣![]() ,反过来,得1﹣
,反过来,得1﹣![]() =(1﹣
=(1﹣![]() )(1+
)(1+![]() )= × ;
)= × ;
③(1﹣![]() )(1+
)(1+![]() )=1﹣
)=1﹣![]() ,反过来,得1﹣
,反过来,得1﹣![]() = =
= =![]() ;
;
利用上面的材料中的方法和结论计算下题:
(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )……(1﹣
)……(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com