练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
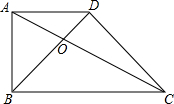
    16．如图，已知梯形ABCD，AD∥BC，对角线AC与BD相交于点O，S△AOD=9，S△BOC=16，求S梯形ABCD．

    分析 由平行线得出△AOD∽△COB，得出面积比等于相似比的平方，求出OA：OC，得出△DOC的面积和△AOB的面积，即可得出梯形ABCD的面积．

    解答 解：∵AD∥BC，
    ∴△AOD∽△COB，
    ∴$\frac{{S}_{△AOD}}{{S}_{△COB}}$=$\frac{9}{16}$，
    ∴$\frac{OA}{OC}$=$\frac{3}{4}$，
    ∵$\frac{{S}_{△AOD}}{{S}_{△DOC}}$=$\frac{OA}{OC}$=$\frac{3}{4}$，
    ∴S△DOC=12，
    ∴S△AOB=S△DOC=12，
    ∴梯形ABCD的面积=S△DOC+S△AOB+S△COB+S△AOD=9+12+12+16=49．

    点评 本题考查了梯形的性质、相似三角形的判定与性质、三角形的面积关系；熟练掌握梯形的性质，并能进行推理计算是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．日升中学七（1）班共有51人，外出参加植树活动，根据任务的不同，分成甲、乙、丙三个小组，甲，乙两小组的人数比为1：2，乙、丙两小组人数之比为3：4．求甲，乙、丙三个小组各有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知（m-53）（m-47）=24，求（m-53）2+（m-47）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于点A（-1，0）、B（3，0），直线y=kx+1与抛物线相交于A、C两点
    （1）求抛物线y=$\frac{1}{2}$x2+bx+c和直线AC的解析式；
    （2）以AC为直径的圆与y轴交于两点M、N，求M、N两点的坐标；
    （3）在抛物线的对称轴上是否存在一点P，△ACP的内心也在对称轴上，若存在，求点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，已知抛物线y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+3交x轴于A，B两点（A在B的左侧），交y轴于C点，抛物线上有一点M，横坐标为4．
    （1）求△ACM的面积；
    （2）在直线OM下方抛物线上有一点N，使∠MON=45°，求N的横坐标；
    （3）在（2）条件下，将∠MON绕O逆时针旋转，旋转过程中，射线OM，射线ON交直线BC分别为E，F，将△OEF沿OE翻折得到△OEG（G为F的对应点），连接CG，若CE：CG=3：4，求线段CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

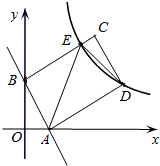    1．如图，矩形ABCD的顶点A、B分别在x轴、y轴上，AD=2AB，直线AB的解析式为y=-2x+4，双曲线y=$\frac{k}{x}$（x＞0）经过点D，与BC边相交于点E．
    （1）填空：k=40
    （2）连接AE、DE，试求△ADE的面积；
    （3）在x轴上是否存在点P，使得△PCD的周长最小？若存在，求出点P坐标及此时△PCD周长的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，若△ABC≌△ADE，且∠B=60°，∠C=20°则∠DAE=100°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

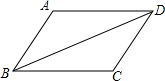    5．如图所示，BD是四边形ABCD的对角线，AD∥CB，请添加一个条件，使△ABD≌△CDB，这个添加的条件可以是AD=CB．（只需填一个，不添加辅助线）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．用四舍五入法，把数4.803保留三个有效数字，得到的近似数是（　　）
    A．4.8B．4.80C．4.803D．5.0

    查看答案和解析>>

    同步练习册答案