
分析 (1)由抛物线解析式得出A、B、C的坐标,算出M点的坐标,由A、M坐标算出直线AM的解析式,AM与y轴的交点设为D,则A与M横坐标之差的绝对值作为水平宽,C与D的纵坐标之差作为铅垂高,$\frac{1}{2}$×水平宽×铅垂高就是△ACM的面积;
(2)只要确定ON所在直线的解析式即可,过点M作MH⊥x轴于点H,MJ⊥y轴于点J;作BK⊥MJ于点K,交OM于点L,ON交直线MJ于点I,这样OBKJ就是正方形,而∠MOI=45°,也就是经典的大角夹半角模型,易证BL+IJ=IL,故设IJ为未知数,将三角形ILK的三边分别表示出来,即可用勾股定理列方程解出IJ的长度.只要确定IJ的长度就可确定I点的坐标,从而确定ON的解析式,也就可以确定N点坐标.
(3)分三种情况讨论:①E在线段BC上,CB延长线上;②E、F均在线段BC上;③E在BC延长线上,F在线段BC上.三种情况都是经典的大角夹半角模型(或变形),每种情况都可证三角形CEG是直角三角形,证法几乎完全一样,只需证一次,后面同理即可,由给定的比例关系确定CE与BC的比例关系就可求出CE的长度.
解答 解:(1)如图1,连接AC、CM、AM,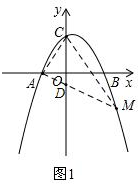
设AM与y轴交于点D,
∵点M在抛物线上,且横坐标为4,
∴M(4,-3),
∵y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+3=$-\frac{1}{2}({x}^{2}-x-6)=-\frac{1}{2}(x-3)(x+2)$,
∴A(-2,0),B(3,0),
设直线AM的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=0}\\{4k+b=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-1}\end{array}\right.$.
∴直线AM的解析式为:$y=-\frac{1}{2}x-1$,
∴D(0,-1),
∵C(0,3),
∴${S}_{△ACM}=\frac{1}{2}×({x}_{M}-{x}_{A})({y}_{C}-{y}_{D)}$=$\frac{1}{2}×6×4$=12;
(2)如图2,过点M作MH⊥x轴于点H,MJ⊥y轴于点J;作BK⊥MJ于点K,交OM于点L,作∠MOI=45°,OI交MJ于点I,OI的延长交抛物线于点N(未画出,也不用画出,知道∠MON是45°就行);延长MJ至P,使JP=BL,连接OP.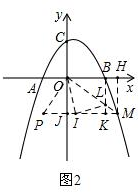
∵M(4,-3),
∴MH=OJ=BK=3,OH=MJ=4,
∵B(3,0),
∴OB=JK=BK=OJ=3,KM=1,
∴OBKJ是正方形,
∵BL=JP,
在△PJO和△LBO中,
$\left\{\begin{array}{l}{OJ=OB}\\{∠OJP=∠OBL}\\{JP=BL}\end{array}\right.$,
∴△PJO≌△LBO(SAS),
∴OP=OL,∠POJ=∠LOB,
∵∠IOL=45°,
∴∠JOI+∠BOL=45°,
∴∠JOI+∠POJ=45°,
∴∠POI=∠LOI,
在△POI和△LOI中,
$\left\{\begin{array}{l}{OP=OL}\\{∠POI=∠LOI}\\{OI=OI}\end{array}\right.$,
∴△POI≌△LOI(SAS),
∴IL=PI=PJ+IJ=IJ+BL,
∵KM=1,OB=3,
∴$\frac{BL}{LK}=\frac{3}{1}$,
∴BL=$\frac{3}{4}BK=\frac{9}{4}$,$LK=\frac{1}{4}BK=\frac{3}{4}$,
设IJ=t,则IL=t+$\frac{9}{4}$,IK=3-t,
在直角三角形LKI中,由勾股定理可知:
$(t+\frac{9}{4})^{2}=\frac{9}{16}+(3-t)^{2}$,解得t=$\frac{3}{7}$,
∴I($\frac{3}{7}$,-3),
∴直线ON的解析式为:y=-7x,
由$\left\{\begin{array}{l}{y=-7x}\\{y=-\frac{1}{2}{x}^{2}+\frac{1}{2}x+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{15+\sqrt{249}}{2}}\\{y=\frac{-105-7\sqrt{249}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{15-\sqrt{249}}{2}}\\{y=\frac{-105+7\sqrt{249}}{2}}\end{array}\right.$(舍去),
∴N点的坐标为($\frac{15+\sqrt{249}}{2}$,$\frac{-105-7\sqrt{249}}{2}$);
(3)①如图3,E点B点上方,F点在B点下方,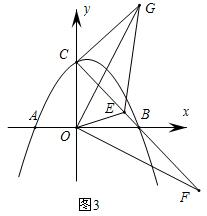
∵∠EOG=∠EOF=45°,
∴∠COG+∠BOE=45°=∠BOF+∠BOE,
∠COG=∠BOF,
∵OC=OB,OG=OF,
在△COG与△BOF中:
$\left\{\begin{array}{l}{OC=OB}\\{∠COG=∠BOF}\\{OG=OB}\end{array}\right.$
∴△COG≌△BOF(SAS),
∴BF=CG,∠OCG=∠OBF=135°,
∵∠OCB=45°,
∴∠ECG=90°,
∵$\frac{CE}{CG}=\frac{3}{4}$,
设CE=3h,CG=4h,则EG=5h,
∴BF=CG=4h,EF=EG=5h,
∴BE=h,
∴CE=$\frac{3}{4}$BC=$\frac{9}{4}$$\sqrt{2}$;
②如图4,E、F在线段BC上,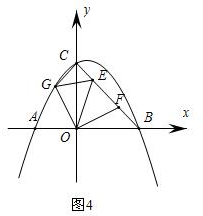
同①可证△OBF≌△OCG,
∴∠GCO=∠FBO=45°,
∴∠GCE=90°,
∵$\frac{CE}{CG}=\frac{3}{4}$,
设CE=3h,CG=4h,
则EG=EF=5h,BF=CG=4h,
∴CE=$\frac{3}{3+4+5}BC=\frac{1}{4}BC$=$\frac{3}{4}\sqrt{2}$;
③如图5,E在BC延长线上,F在线段BC上,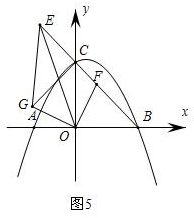
同①可证△OBF≌△OCG,
∴∠GCO=∠FBO=45°,
∴∠GCE=90°,
∵$\frac{CE}{CG}=\frac{3}{4}$,
设CE=3h,CG=4h,
则EG=EF=5h,BF=CG=4h,
∴CF=2h,
∴CE=$\frac{1}{2}BC$=$\frac{3\sqrt{2}}{2}$.
综上所述,CE的长度为$\frac{9}{4}$$\sqrt{2}$或$\frac{3}{4}\sqrt{2}$或$\frac{3\sqrt{2}}{2}$.
点评 本题是一道经典中考压轴题,综合考查了点与抛物线的关系、待定系数法求一次函数解析式、铅垂高法求三角形面积、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理及其逆定理、旋转变换、对称变换、分类讨论等众多的知识点和技能,难度较大.第(1)问当中,对于在平面直角坐标系中求斜三角形的面积,铅垂高法是重要诀窍,这一方法高频地出现在各种与面积有关的压轴题当中,要引起高度重视;第(2)问,要求N点的坐标,其关键在于求出ON所在直线的解析式,将直线解析式与抛物线方程联立即可解出来N点坐标,这里用到的是正方形当中90度夹半角模型,也就是用几何手段确定了直线ON的解析式(连N点都不需要画在图上),方法很巧,值得重视;第(3)问,由于∠MON在旋转过程中位置有三种情况,所以要分类讨论,每一种情况也是大角夹半角(或其变形)旋转模型的应用.纵观本题,其实函数的知识考的不是太多,几何所占的比重更大,是一道考查同学们综合能力的好题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
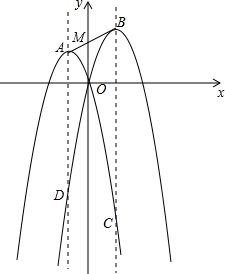 如图,抛物线C1:y=-(x+m)2+m2(m>0)的顶点为A,抛物线C2:y=-(x-n)2+n2(n>m)的顶点为B,抛物线C2的对称轴与抛物线C1相交于点C,抛物线C1的对称轴与抛物线C2相交于点D.
如图,抛物线C1:y=-(x+m)2+m2(m>0)的顶点为A,抛物线C2:y=-(x-n)2+n2(n>m)的顶点为B,抛物线C2的对称轴与抛物线C1相交于点C,抛物线C1的对称轴与抛物线C2相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
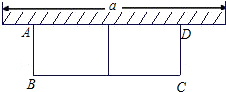 如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).
如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com