
����Ŀ����֪������y=x2+kx+2k��4
��1����k=2ʱ������������ߵĶ������ꣻ
��2����֤������kΪ�κ�ʵ���������߶���x���н��㣬�Ҿ���x��һ���㣻
��3����֪��������x�ύ��A��x1��0����B��x2��0�����㣨A��B����ߣ���|x1|��|x2|����y�ύ��C�㣬��S��ABC=15���ʣ���A��B��C�����Բ����������Ƿ��е��ĸ����㣿��˵�����ɣ�����У���������꣮

���𰸡���1����������Ϊ����1����1������2��֤������������3����1����6����
���������⣺��������![]() ����ʱ��������Ϊ
����ʱ��������Ϊ![]() ��
��![]() ��
��![]() ��������������������������
��������������������������
�䷽�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��������
��������
��![]() ��
��![]() ������
������
������������������������������������������������������������������
��Ҳ���ɶ��㹫ʽ��ã�
��������![]() ��������
��������![]() ��
��![]() ��
��![]() ��4����������������������������������
��4����������������������������������
��һԪ���η��̸����б�ʽ
�S��![]() ��������
��������![]() ��������
��������![]() ��
��![]() ��������
��������![]() ��������������������
��������������������
������![]() Ϊʲôʵ����
Ϊʲôʵ���� ![]() ������
������
����![]() ��
��![]() ��
��![]() ��4�������н⣬������������������������������������
��4�������н⣬������������������������������������
������������![]() ���н��㣮
���н��㣮
�������ʽ��![]() ��
��![]() ������������������������������������������
������������������������������������������
��![]() ����ʱ��
����ʱ�� ![]() ��
��![]() ��
��
![]() 1��
1��![]() ��������
�������� ![]() 2��
2��![]() ����
����![]() ������
������
��![]() ����ʱ��
����ʱ�� ![]() ��
��![]() ��
��
![]() 1��
1��![]() ����
����![]() ������
������ ![]() 2��
2��![]() ��������
��������
����������![]() ��Ľ���ֱ�Ϊ�������������ͣ���
��Ľ���ֱ�Ϊ�������������ͣ���![]() ������������
������������
���㣨������������![]() ���ϵĶ��㣻������������������������������������
���ϵĶ��㣻������������������������������������
�������������£��������Բ����������е��ĸ����㣮������������������
��˵�Ϊ�ģ���| ![]() 1|��|
1|��| ![]() 2|��C����y���ϣ�
2|��C����y���ϣ�
�������ߵĶԳƣ���֪��ò��������ߵĶ��㣮����������������������������
����Բ�������߶�����Գ�ͼ�Σ�
�������¡��������Բ�����������һ����Գ�ͼ�Σ�����������������������
��![]() ���ϵ���������¹��������߶Գ���Գƣ�
���ϵ���������¹��������߶Գ���Գƣ�
���������¡��������Բ�������ߵĵ��ĸ�
�����Ӧ��C����������߶Գ���Գƣ�����������������������������������
����������![]() ��Ľ���ֱ�Ϊ�������������ͣ���
��Ľ���ֱ�Ϊ�������������ͣ���![]() ������������
������������
����������![]() ��������
��������![]() ����ʱ����������������������������
����ʱ����������������������������
����������������������������![]() ������������
������������
��![]() 1��������
1�������� ![]() 2����
2����![]() ������
������
��| ![]() 1|��|
1|��| ![]() 2|�ã�
2|�ã�![]() �������������
�������������![]() ������
������
���ݣ���ABC����������![]() �������ϣã�������
�������ϣã�������
���£���![]() ��������������������
��������������������![]() ��
��
�ϣã�|��![]() ����|��������
����|��������![]() ��
��
��![]() ������
������![]() ����������
����������![]() ����������
����������
����������![]() ������
������
���![]() ��������ȥ����
��������ȥ����![]() ��������
��������
��ʱ�����߽���ʽΪ![]() ��
��![]() ��
��
��Գ���Ϊ![]() ��
��![]() ���õ�����Ϊ��������������
���õ�����Ϊ��������������
������![]() ��
��![]() �ĶԳƵ������Ϊ��������������������������������������������
�ĶԳƵ������Ϊ��������������������������������������������
����������![]() �������ɣ����ڣµ���ߣ�
�������ɣ����ڣµ���ߣ�
֪��������Ϊ����![]() ��������������Ϊ��������������
����������������������������
��![]() 1����
1����![]() ������
������ ![]() 2��������
2��������
����ʱ| ![]() 1|��|
1|��| ![]() 2|��������֪����|
2|��������֪����| ![]() 1|��|
1|��| ![]() 2|�������
2|�������
�������ڴ��������
�ʵ��ĸ����������Ϊ��������������
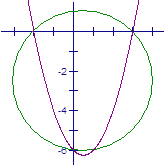
����ͼ����
��������![]() �������������ߣ�ͨ���䷽����ô������ߵĶ�������
�������������ߣ�ͨ���䷽����ô������ߵĶ�������
��2����y=0���ⷽ��![]() ��
��![]() ��
��![]() ��4�����������������x��������ĺ����꣬����Ϊ��kֵ�صĵ㣻
��4�����������������x��������ĺ����꣬����Ϊ��kֵ�صĵ㣻
��3����A��B��C�����Բ���������е��ĸ�����D������A��B��C�������꣬����k�ķ�Χ����ʾ��ABC��������з�����k���ٸ��ݶԳ�����D������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڽ���4�·�ij���ڵ�����������£���λ�棩��26��25��27��28��27��25��25����������ڵ�������µ���������λ���ֱ��ǣ� ��
A.25��26
B.25��26.5
C.27��26
D.25��28
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ�鳤����Ӳֽ������������ͶӰʵ�飬ͨ���۲죬������鳤����Ӳֽ����ƽ���ĵ����ϲ����ܳ��ֵ�ͶӰ�ǣ�������
A.������
B.�߶�
C.����
D.ƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ������صĺ��θ߶ȷֱ�Ϊ20m����15m�ͩ�10m����ô��ߵĵط�����͵ĵط��ߣ�������
A.5m
B.10m
C.25m
D.35m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ǵ���ǵ�3��������ǵIJ��Ǵ�18�㣬������ǵĶ���Ϊ��������
A. 36��B. 18��C. 54��D. 27��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̲�ĸ�⡡��P(x��y)�ڵ�һ���ޣ���x��y��8����A������Ϊ(6��0)�����OPA�����ΪS.
(1)�ú���x��ʽ�ӱ�ʾS��д��x��ȡֵ��Χ����������S��ͼ��
(2)����P�ĺ�����Ϊ5ʱ����OPA�����Ϊ���٣�
(3)��OPA������ܴ���24��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x��һԪ���η��̣���m��1��x2+��m��2��x��1=0��mΪʵ������
��1������������������ȵ�ʵ��������m��ȡֵ��Χ��
��2����![]() �Ǵ˷��̵�ʵ������������y=��m��1��x2+��m��2��x��1��x�ύ��A��B�������ߵĶ���ΪC�����ABC�������
�Ǵ˷��̵�ʵ������������y=��m��1��x2+��m��2��x��1��x�ύ��A��B�������ߵĶ���ΪC�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ִ���30����/Сʱ���ٶ��������У�;�нӵ�̨�羯����̨����������60����/Сʱ���ٶ��������ƶ�����̨������20�����Բ���������߽磩������̨���������ִ���A��ʱ�����̨�������Ƶ�λ�ڵ�A���Ϸ����B������AB=40���
��1�����ִ���ԭ����ԭ�ٶȼ������У�
�ٴ������֣���̨�����ĵ���A��ʱ���ִ��϶���Ӱ�죬Ϊʲô��
�����ִ���A��������������̨���ʱ�䣻
��2�����ִ���A��Ѹ�ٸı亽�ߣ���ƫ��60���ķ���ıܷ����30����/Сʱ���ٶ�ʻȥ���ִ�������ܵ�Ӱ�죿���ᣬ�����ִ��������̨���ʱ�䣻�����ᣬ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() �֣�
�֣�
��ͼ����![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת��
����ʱ�뷽����ת��![]() ��
�� ![]() �������Ϊ
�������Ϊ![]() ��
��

��![]() ����
����![]() ������꣮
������꣮
��![]() �����
�����![]() ��
�� ![]() ��
�� ![]() �����������
�����������![]() �Ľ���ʽ��
�Ľ���ʽ��
��![]() ���ڣ�
���ڣ�![]() ���е����������Ƿ���ڵ�
���е����������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��
�� ![]() ��
�� ![]() Ϊ������������ǵ���ֱ�������Σ���
Ϊ������������ǵ���ֱ�������Σ���
���ڣ�������е�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com