
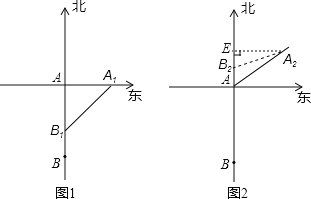
【题目】如图,一艘轮船以30海里/小时的速度由西向东航行,途中接到台风警报,台风中心正以60海里/小时的速度由南向北移动,距台风中心20海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向的B处,且AB=40海里.
(1)若轮船以原方向、原速度继续航行:
①船长发现,当台风中心到达A处时,轮船肯定受影响,为什么?
②求轮船从A点出发到最初遇到台风的时间;
(2)若轮船在A处迅速改变航线,向北偏东60°的方向的避风港以30海里/小时的速度驶去,轮船还会不会受到影响?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.

【答案】(1)①会受影响,理由见解析;②轮船从A点出发到最初遇到台风的时间是![]() 小时;(2)轮船从A点出发到最初遇到台风的时间是
小时;(2)轮船从A点出发到最初遇到台风的时间是![]() 小时.
小时.
【解析】试题分析:(1)①求出当台风中心到达A处时,所用时间,进而求出轮船此时驶离A处距离,比较即可;
②当轮船在t小时后到达A1时,最初遇到台风,此时台风中心到达B1,进而表示出各线段长,再利用勾股定理求出即可;
(2)当轮船在m时后到达A2时,最初遇到台风,此时台风中心到达B2,进而得出A2B2=20,A2A=30m,AB2=60m-40,作A2E⊥AB2,垂足为E,则A2E=15![]() m,AE=15m,EB2=AE-AB2,再利用勾股定理求出即可.
m,AE=15m,EB2=AE-AB2,再利用勾股定理求出即可.
试题解析:(1)①会受影响,
当台风中心到达A处时,用时: ![]() (小时),
(小时),
则轮船此时驶离A处:30×![]() =20(海里),因此轮船肯定受影响;
=20(海里),因此轮船肯定受影响;
②如图1,若轮船在t小时后到达A1时,最初遇到台风,此时台风中心到达B1,
则A1B1=20海里,A1A=30t,AB1=40﹣60t,
由勾股定理知,(30t)2+(40﹣60t)2=202,
解得:t1=![]() ,t2=
,t2=![]() ,
,
则轮船从A点出发到最初遇到台风的时间是![]() 小时;
小时;
(2)会,理由:如图2,若轮船在m时后到达A2时,最初遇到台风,此时台风中心到达B2,则A2B2=20,A2A=30m,AB2=60m﹣40,作A2E⊥AB2,垂足为E,则A2E=30m ×sin60°=15![]()
m,AE=15m,EB2=AE﹣AB2=15m﹣(60m﹣40)=40﹣45m,
由勾股定理得:(15![]() m)2+(40﹣45m)2=202,
m)2+(40﹣45m)2=202,
解得:m1=m2=![]() ,
,
则轮船从A点出发到最初遇到台风的时间是![]() 小时.
小时.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+kx+2k﹣4
(1)当k=2时,求出此抛物线的顶点坐标;
(2)求证:无论k为任何实数,抛物线都与x轴有交点,且经过x轴一定点;
(3)已知抛物线与x轴交于A(x1,0)、B(x2,0)两点(A在B的左边),|x1|<|x2|,与y轴交于C点,且S△ABC=15.问:过A,B,C三点的圆与该抛物线是否有第四个交点?试说明理由.如果有,求出其坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
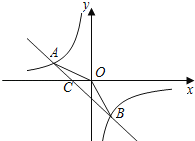
【题目】如图,在平面直角坐标系xOy中,若点A(﹣2,n),B(1,﹣2)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标;
(3)求点O到直线AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)阅读下列材料:
(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com