Question

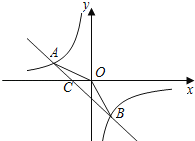
【题目】如图，在平面直角坐标系xOy中，若点A（﹣2，n），B（1，﹣2）是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点．

（1）求反比例函数和一次函数的解析式；

（2）求直线AB与x轴的交点C的坐标；

（3）求点O到直线AB的距离．

Answer 1

【答案】（1）反比例函数的解析式为y=﹣，一次函数的解析式为y=﹣x﹣1；（2）点C（﹣1，0）；（3）点O到直线AB的距离为．

【解析】试题分析：（1）根据点B的坐标求出反比例函数解析式，根据反比例函数得出点A的坐标，最后根据A、B的坐标得出一次函数解析式；（2）令y=0得出点C的坐标；（3）利用面积法求出点O到直线的距离．

试题解析：（1）∵点B（1，－2）在函数y=的图象上，∴， 得：m=－2．

∴反比例函数的解析式为y=－．

∵点A（－2，n）在函数y=－的图象上， ∴得：n=1．∴A（－2，1）

∵y=kx+b经过点A和点B ∴解得：

∴一次函数的解析式为y=－x－1．

（2）在一次函数的解析式y=－x－1中，令y=0得x=－1．∴点C的坐标为（－1，0）．

（3）设点到直线AB的距离为直线AB与轴相交于，则．

则： ．

点到直线AB的距离为．